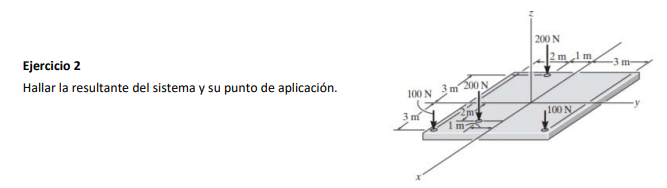
Buenas tardes, le escribo porque tengo una consulta con este ejercicio, ya calcule la fuerza resultante y calcule los versores de dicha fuerza resultante, pero la hora de buscar el punto de aplicación de la resultante no tengo muy en claro como hacerlo, como se haría?
Buenas tardes,
Para calcular el punto de aplicación de la resultante tenes que plantear una igualdad de momentos; el momento de R respecto al origen (o respecto a cualquier otro punto) debe ser igual a la suma de los momentos respecto a ese mismo punto, que genera cada fuerza.
r x R = r1 x F1 + r2 x F2 + r3 x F3 + r4 x F4
Podes plantear la ecuación vectorial o lo podes plantear directamente como dos ecuaciones escalares, que serian los momentos respecto a cada eje (x e y). Resolviendo, obtenes las coordenadas x e y del punto de aplicación de la resultante.
Hola Dalma, como andas? justo aprovechando la consulta del ejercicio 2, yo lo pude resolver pero me surgió una duda..
Cuando queremos sacar la fuerza resultante en este ejercicio (obviamente solo en componente z), la pensamos como en modulo, no? me refiero a no darle sentido negativo porque apunta hacia abajo digamos.
Voy con esta consulta por el lado de que al tomar momentos de cada fuerza respecto del eje "x" como "y", lo que hay que hacer en síntesis es fuerza (en modulo positivo) por distancia? solamente el signo lo va a dar el momento? porque creo que antes había cometido el error de darle sentido negativo a cada fuerza y además le había puesto el signo correspondiente al momento y daba vuelta todo.
Gracias!
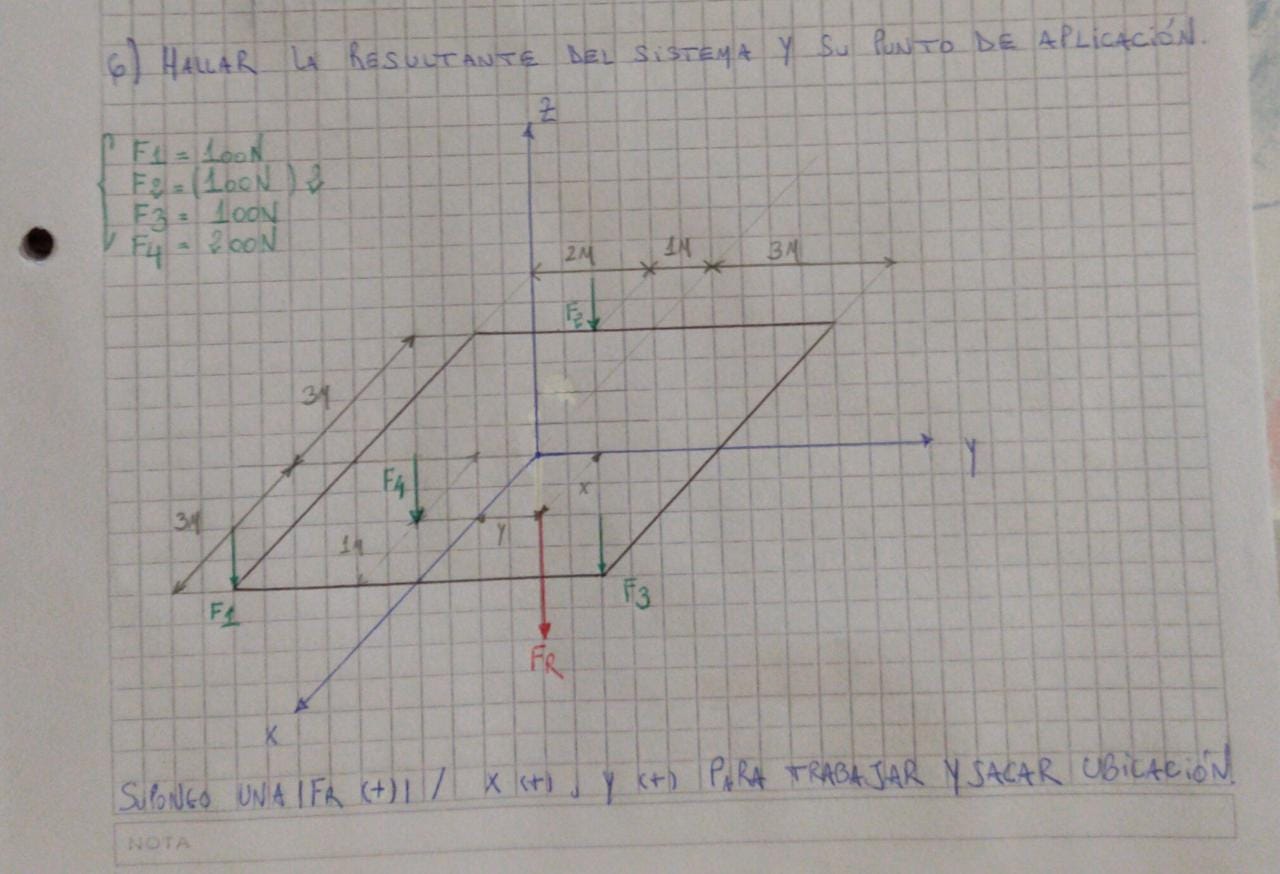
Foto de la resolución

Hola Matias,
Siempre que se pida calcular una fuerza, hay que dar como resultado su magnitud y su dirección, pero a la hora de plantear los momentos respecto a cada eje, lo planteamos como vos decís: es la fuerza (en módulo) por el brazo de palanca y el signo lo colocas de acuerdo a si el momento es positivo o negativo.
Te hago un comentario: planteaste todo bien pero al final te olvidaste del signo menos cuando despejaste y (y= - MRx/FR)
Uh cierto, excelente!
Gracias Dalma.
