Buenos días profesores, estoy teniendo algunas dudas con el cálculo de la TF de una función f(t) mediante la resolución de la integral impropia. Plantie dos situaciones, una para los w<0 con un camino y otra para los w>0 con otro camino y pude justificar que la integral sobre la curva de los caminos era cero utilizando el Teorema de Jordan. Lo que me hace ruido es que obtuve un resultado distinto en signo de F(w) para cada w, entonces creo que algo de lo que estoy planteando este mal pero no logro identificar que. Me sería de gran ayuda si alguien puede ver el error.
Muchisimas gracias!



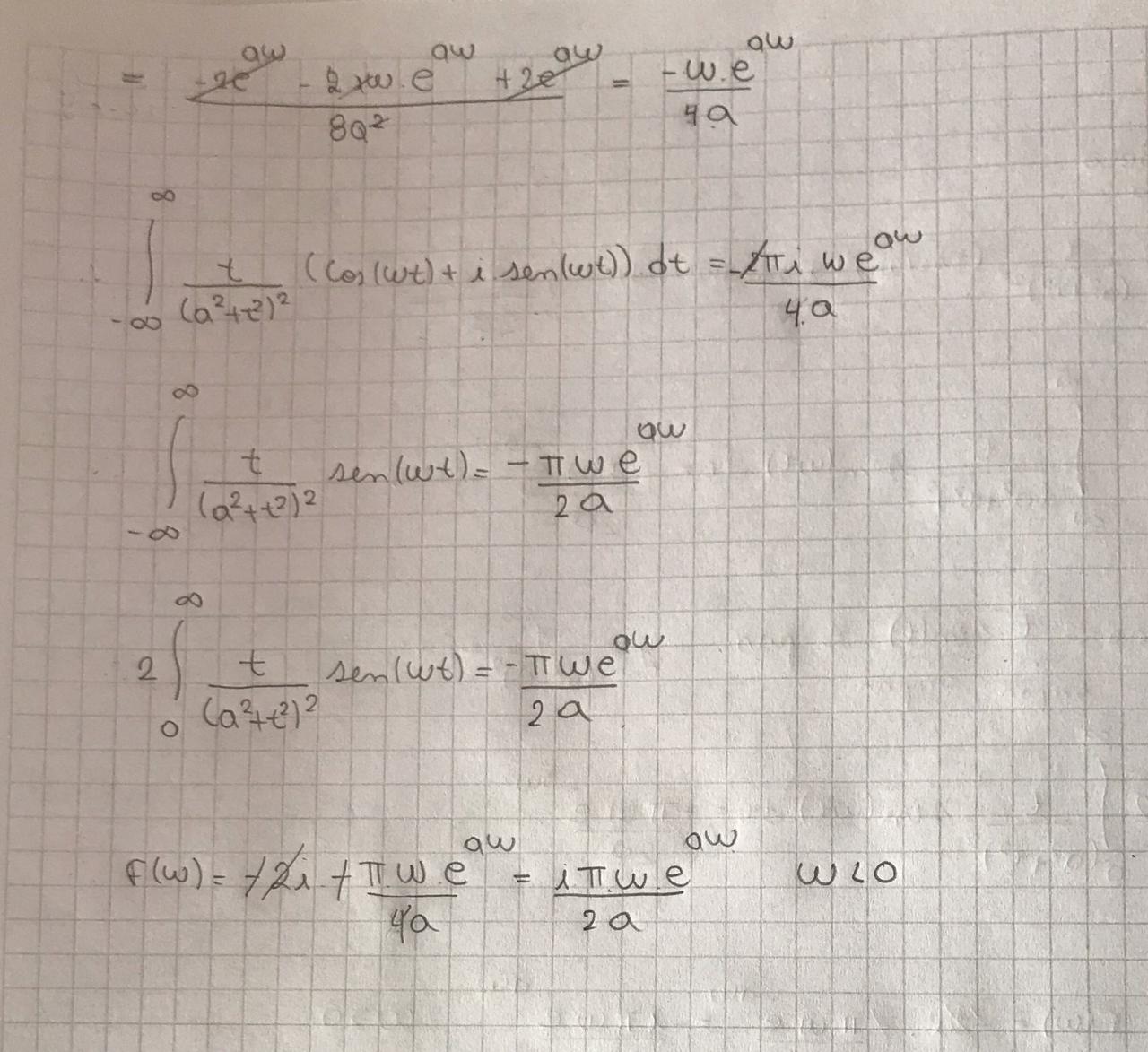
Hola Andrea.
Yo no veo error en lo que hacés, si querés, la transformada la podés dejar expresada como una -a|w| (menos "a" por módolo de w). Pensá que tanto para w tendiendo a mas infinito como a menos infinito la transformada tiene que irse a cero por estar la función original en L1, y además está en L2, con lo que también vale la proporcionalidad entre las normas 2 de f (t) y F(w)... no puede irse a infinito con lo que el signo del exponente tiene que ser negativo en ambos casos.
Hola Julián!! Muchísimas gracias por responder. Entiendo que la variación del signo dentro de la exponencial se puede solucionar con -a|w|, pero es correcto que F(w) para w>0 tenga un signo menos adelante mientras que F(w) para w<0 no?
F(w)= - (i*pi*w*e^-a|w|)/2a para w>0
F(w)= (i*pi*w*e^-a|w|)/2a para w<0
Allí también (donde esta la w) debería poner |w| o es un error de alguna cuenta esa variación del signo?
Hola Andrea, perdón ahora si entendí la consulta.
Hay un error de signo.
F(0) es la integral de f en toda la recta. Además la función f es continua e integrable, por lo que la transformada debe ser una función continua...
Me parece que en caso w<0, te está faltando cambiarle el signo al valor de la integral, poque la recorrés en sentido negativo...
Avisame si era eso.
Saludos
Muchas gracias por responder un sábado Julián. Me parece que era eso, no me había dado cuenta que había que modificarle el signo a la integral. Igualmente hay otro ejercicio que resolví de la misma manera y llegue a buen resultado sin haber cambiado ese signo, así que me marea un poco, pero ahora voy a ir revisando bien las cuentas.
De nuevo, muchísimas gracias y saludos!
