Buen día, estaba intentado realizar el ejercicio 1.7 y me surgieron dudas sobre cómo armar 2 restricciones. En el enunciado me dice que hay una limitación sobre la cantidad de autos y camiones a estampar, pero no sabia cómo representar dicha restricción de forma gráfica (sucede lo mismo con la del montaje de motores).
Considero que tengo que armar la relación lineal y a partir de eso ver de forma gráfica cómo influye con el resto de las limitaciones, pero no logro darme cuenta como realizarla.
Adjunto la imagen del ejercicio.
Desde ya muchas gracias,
saludos.

Buenos dias Agustin,
La idea seria definir un consumo en Ta HE/auto y Tc HE/camión entonces:
Ta HE/auto.XA + Tc HE/camión.Xc ≤ HE disponibles /año
También se sabe que:
Ta HE/auto * 25000 autos = HE disponibles /año
Tc HE/camión * 40000 camiones = HE disponibles /año
Reemplazando:
(HE disp /año)/ 25000 autos * XA + (HE disp /año)/ 40000 camiones* Xc ≤ HE disp /año
Luego se simplifica, obteniendo:
XA / 25000 autos + Xc / 40000 camiones ≤ 1
Saludos,
Agustin Compagnucci.
Hola Agustín, agregando a lo que ya te respondieron, comparto el razonamiento que use para completar este ejercicio y el resultado obtenido:
Estampado:
Sabiendo que la fabricación de un auto insume mas recursos de estampado, a razón de 40.000/25000 = 1,6
=> la restricción del área de estampado queda planteada asi:
1,6 * XA + XC =< 40000
Análogamente, para el área de Montaje de Motores:
(en este caso, el montaje de motor de un auto insume la mitad de recursos que un motor de camion)
0,5 * XA + XC =< 16667
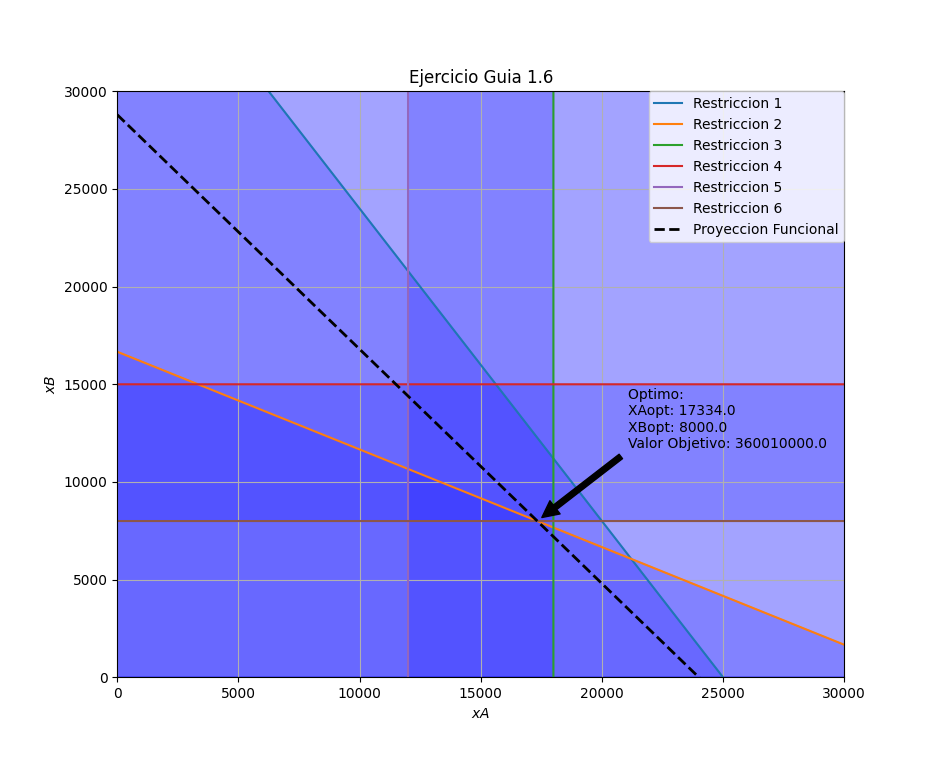
Adjunto la imagen de la resolución grafica, que me dio como optimo:
- 17334 Autos
- 8000 Camiones
- Beneficio Total = $ 360.010.000
Hola Sebastian, cuál es la librería que usaste para graficar la solución?
Saludos,
Julia
Excelentes aportes! felicitaciones.
Buenas, para graficar use matplotlib.pyplot
Comparto el código que use en python.
