Buenas noches.
Sí, esa forma que decís es posible y como decís un poco extraña (se resume a un ejercicio de análisis II, con teorema de la función implícita sale).
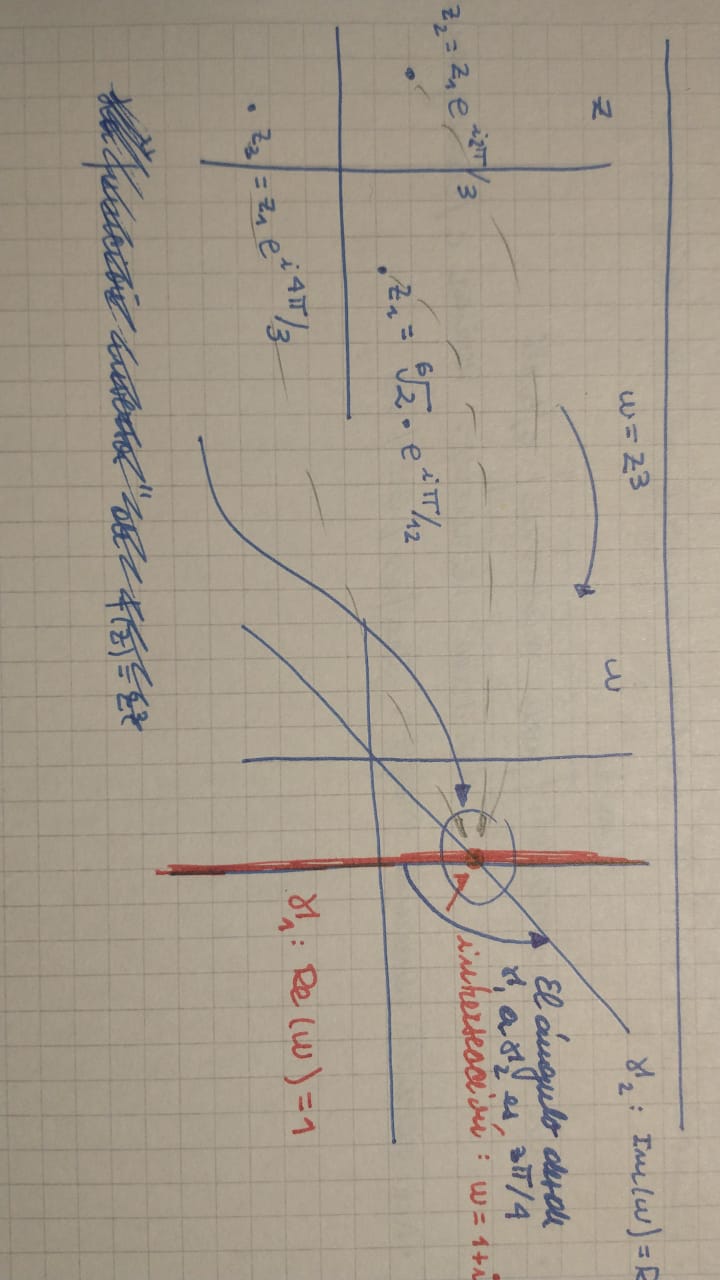
Te dejo una foto y una justificación de por qué si hacer cuentas ese ángulo es 3pi/4...
Suponé primero que hay dos curvas "originales", que se transforman por la función f(z)=z^3 y que en el plano w, luego de transformarse, se ven como Re(w)=1 y Re(w)=Im(w).
Ahora bien, en el plano w se cortan en el punto 1+i, que puede corresponder a 3 raices en el plano complejo...
Cualquiera sea esa raiz, la transformación w=z^3 es conforme en ese punto, por lo tanto también va a existir una función inversa local que también será conforme...
Y ahí te le dejo picando... con eso y un poco de imaginación terminás de justificar que el ángulo de las curvas originales (o de las curvas del plano w luego de ser tranformadas por la "inversa local) no va a cambiar. Si no se te ocurre cómo lo vemos. Es rebuscado pero "sin cuentas".
Saludos
Julián