Buenas, tengo dos preguntas con respecto a este ejercicio.
Primero, como en este caso hay 3 chapas, hay 5 grados de libertad, pero encuentro 6 condiciones de vinculo, dos del punto fijo, dos por las bielas y dos por los dos puntos móviles, por ende seria un sistema hiperestatico. De ser así, se puede segur resolviendo el ejercicio para encontrar las reacciones de vinculo?
Segundo, no entiendo cómo interpretar la fuerza distribuida de 2kN/m ubicada a la izquierda de la primer chapa en forma vertical.
Muchas gracias.
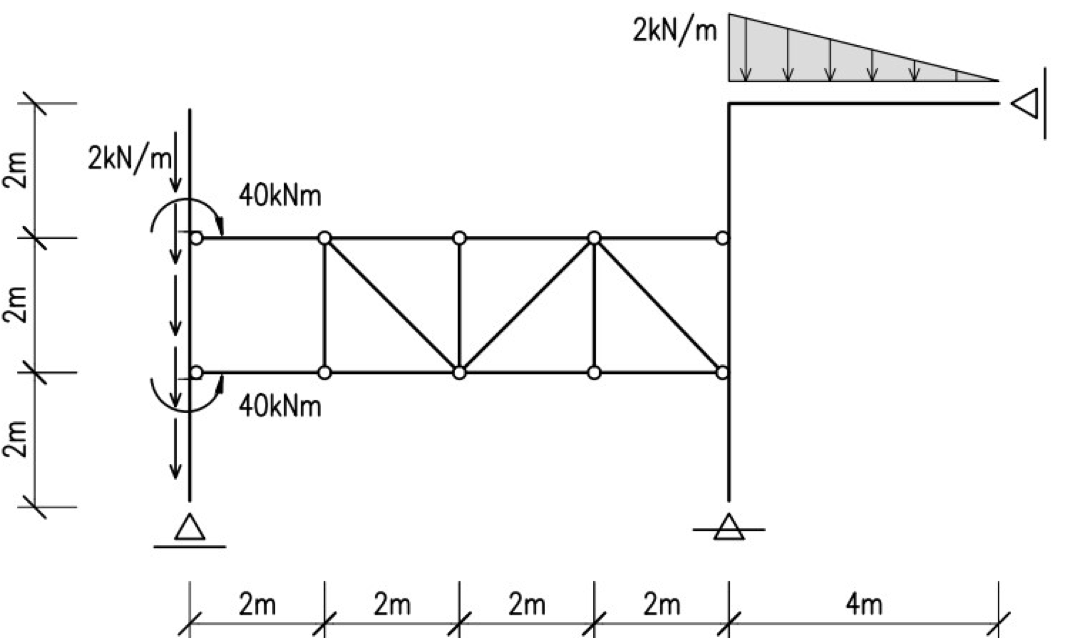
Hola Franco, como estas? En esta estructura hay dos chapas y dado que es una cadena abierta debe haber 4 condiciones de vinculo externo para que el sistema sea isoestaticamente estable, las cuales están.
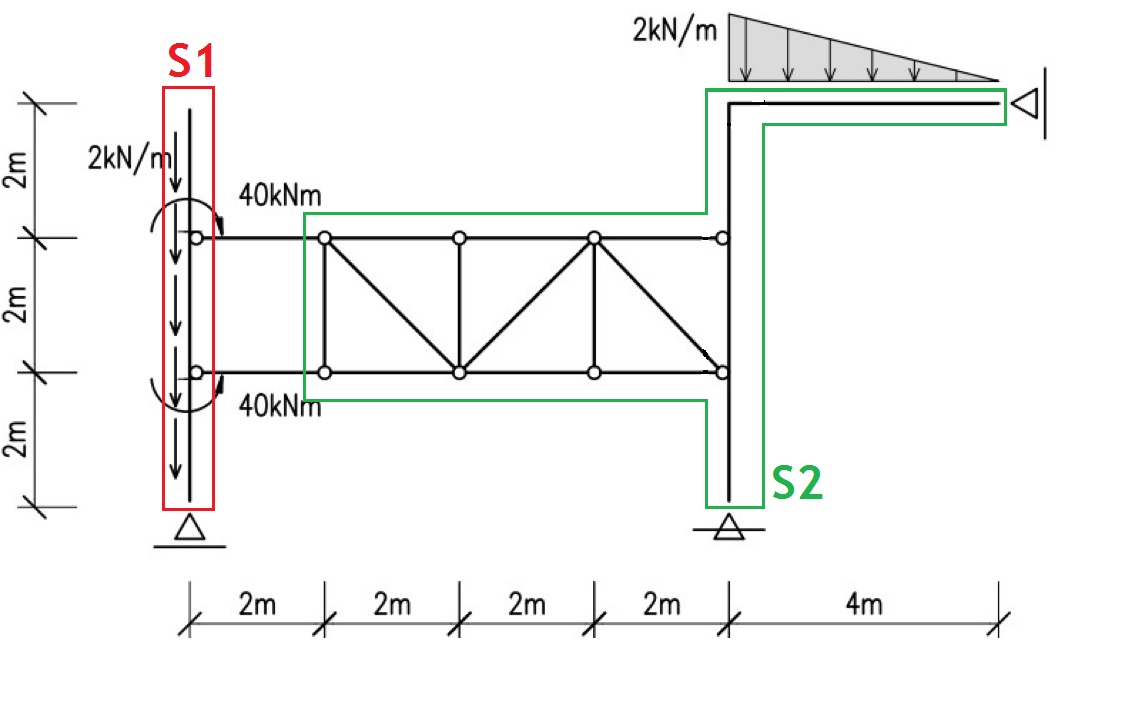
Notemos lo siguiente, la barra vertical es una chapa como bien identificaste, la cual esta unida por dos bielas paralelas a una estructura conformada por triangulos, dado que las bielas unen partes de la estructura estas son vinculos internos por lo que no se cuentan a la hora de ver si un sistema es isotatico o no. Continuando vemos que estas dos bielas unen a la chapa vertical con un conjunto integramente conformado por triangulos que a su vez esta unido a una chapa con forma de L invertida. Veamos lo siguiente,
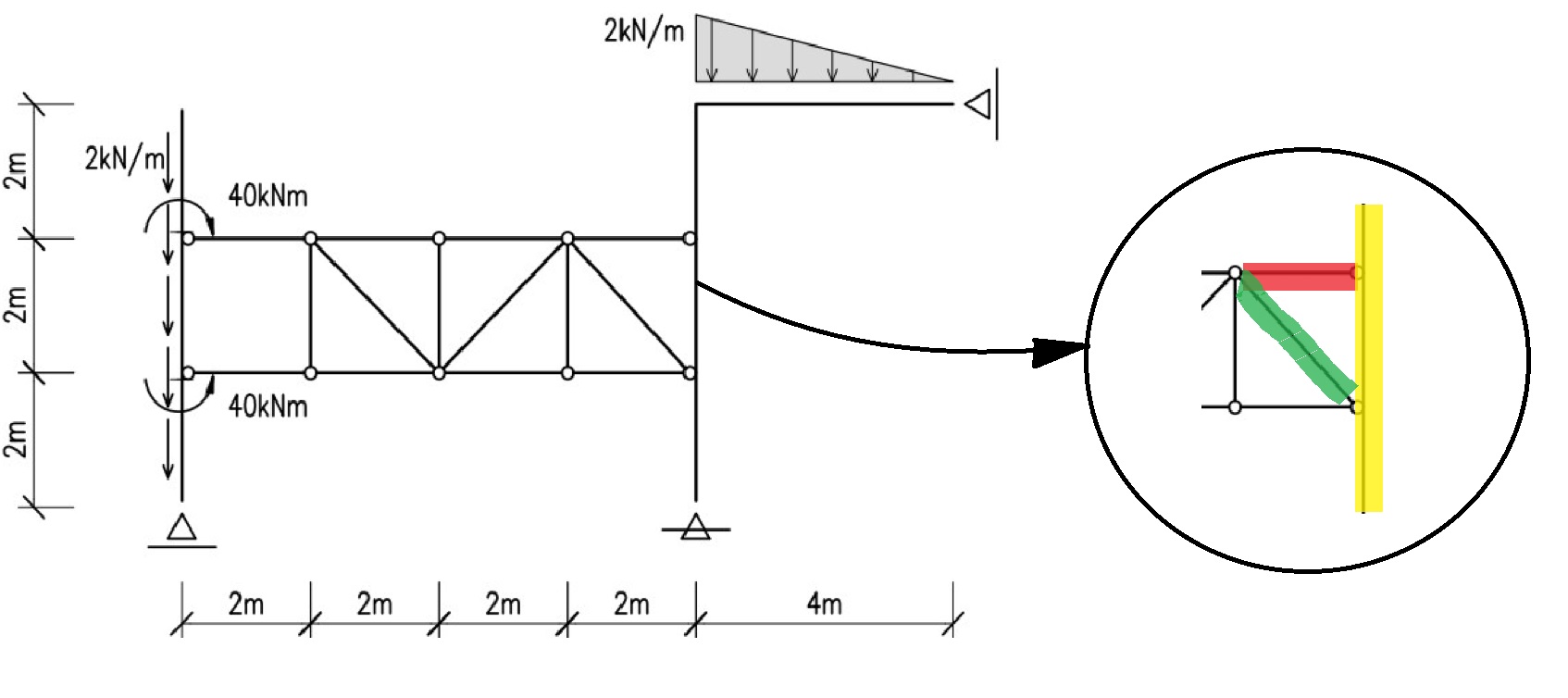
Ahi se ve como las "chapitas" roja y verde forman un con la chapa amarilla un arco de tres articulaciones no alineadas, de tal forma todo eso se comporta como un único cuerpo rigido y dado que todas las barras que se unen continuan con la estrucutra de triangulo, el cuerpo de la L invertida y el conjunto de triangulos (que mas adelante llamaremos reticulado) se puede considerar como un único cuerpo rigido.
Luego, el sistema tiene dos chapas y 4 condiciones de vinculo externo y es un sistema isoestaticamente sustentado.
Por otro lado la fuerza de 2/kN aplicada en la chapa S1 es una fuerza distribuida como las que veniamos viendo con la diferencia que esta aplicada en el direccion del eje de la barra.
Avisame si te quedo alguna duda, saludos,
Lucía.
Perfecto Lucia muchas gracias, lo único que no me queda claro es lo da la fuerza distribuida en la chapa s1, cual seria la resultante en ese caso? q x L?
Y ya que estoy aprovecho para consultarte sobre otro ejercicio parecido que no me cierra, es del mismo ejercicio 7 pero otra estructura, en este caso identifique 3 chapas, y el análisis cinematico : " S1 tiene un apoyo fijo y uno móvil cuya recta de acción no interseca al fijo, por ende S1 se encuentra inmóvil. Ademas el punto fijo de S1 le proporciona una biela ficticia a S2. Por otro lado la chapa S3 tiene un apoyo fijo y le proporciona otra biela ficticia a S2. Luego la chapa S2 posee tres apoyos móviles "
El único problema de este análisis es que los apoyos móviles de S2 concurren en un punto. No estoy seguro de si el apoyo móvil es compartido para ambas chapas o si debería tomar todo el conjunto como una sola chapa.
Muchas gracias.
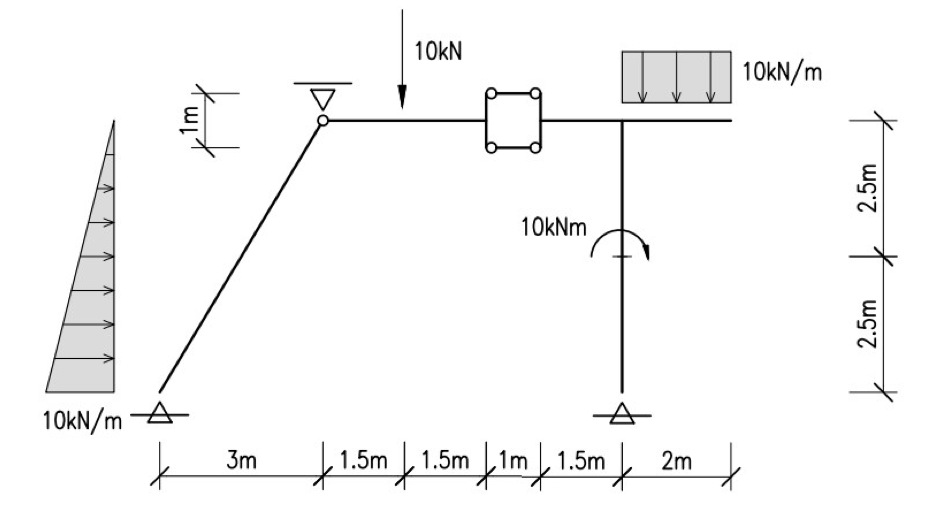
Vamos primero con la nueva estructura que mandaste,
como bien dijiste, la estructura tiene 3 chapas y dado que es una cadena abierta debe tener 5 condiciones de vinculo aplicadas, vemos que hay dos apoyos fijos y un apoyo movil por lo que la estructura es isoestatica.
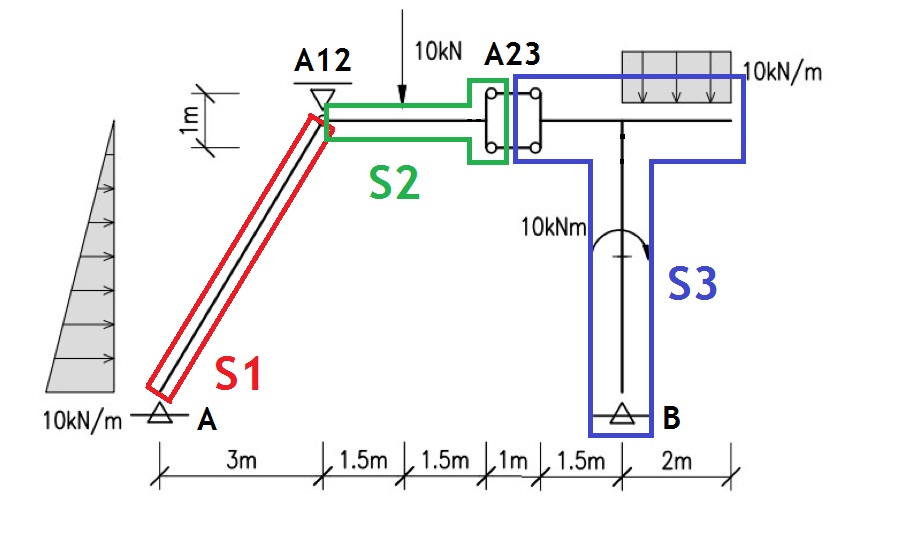
Ahora veamos si hay o no vinculacion aparente [VER FOTO 1]
La chapa [S1] tiene aplicado un apoyo fijo en A y un apoyo movil en A12 y dado que la articulación pertenece tanto a [S1] como a [S2], la chapa [S1] está fija. Luego como, A12 pertenece a [S2], ya encontramos es un punto fijo de [S2]. Despues vemos que [S3] tiene un apoyo y, luego, el punto fijo de [S2], A12, con el apoyo fijo de [S3], B, y las bielas paralelas forman un arco de tres articulaciones no alineadas y tanto [S2] como [S3] también están fijas.
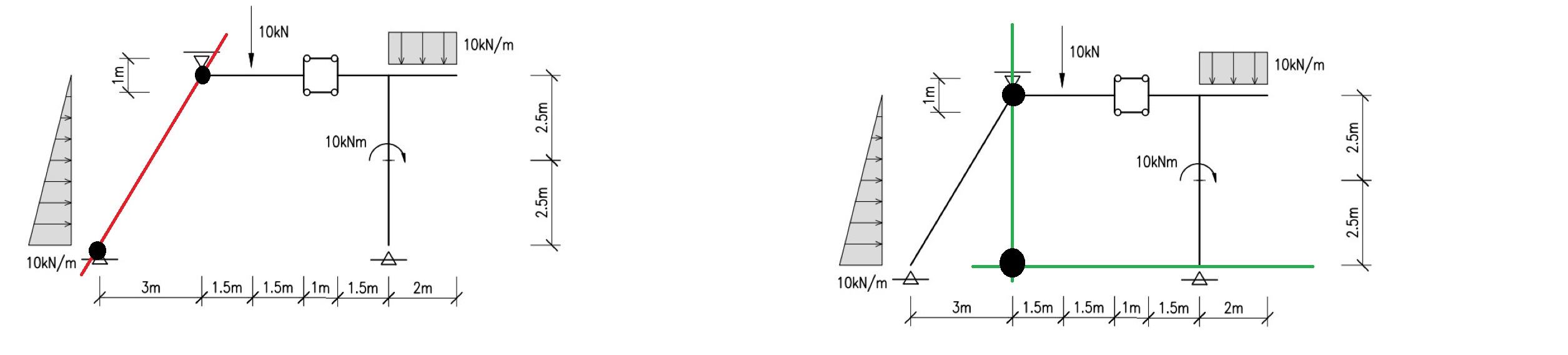
Ese es un posible analisis cinematico, ahora vamos con otro posible analisis [VER FOTO 2]
Vemos que [S1] (roja) tiene un apoyo fijo, luego, dado que tiene aplicado un apoyo movil en A12 y su recta de acción no pasa por el apoyo fijo la chapa [S1] esta fija y por lo tanto la articulación A12 esta fija. Luego A12 es un punto fijo de [S2]. Para encontrar el otro punto fijo de [S2] sabemos que primero tenemos que extender la recta de acción del apoyo movil de [S2], luego, tenemos que encontrar el apoyo movil que le da el apoyo fijo que tenemos en [S3], de tal forma tenemos que extender una recta desde el apoyo fijo de [S3] que pase por la articulacion A23 (bielas) y que corte a la recta del apoyo movil de [S2]. Dado que las bielas paralelas concurren al impropio horizontal trazamos una recta que pase por el apoyo fijo de [S3] y que corte a la del apoyo movil de [S2] y, donde se cortan, está el otro punto fijo de [S2]. Luego [S2] está fija. Finalmente, [S3] tiene un apoyo fijo y las bielas le proporcionan cada una un apoyo movil y, luego, [S3] tiene más de un punto fijo y [S3] esta fija.
Notemos tambien que en la primer parte de este segundo analisis cinematico, tambien podes decir que como [S1] esta fija por que el apoyo movil no pasa por el punto fijo de esta, tiras una recta desde el apoyo fijo de [S1] que pase por la articulación A12 y corte al apoyo movil de [S2] y dicho punto, que es justamente A12, es un punto fijo de [S2].
Decime si te aclare la duda, saludos,
Lucia.
Me falto responderte lo de la carga distribuida! Si, como decis, la resultante es q.L y esta aplicada en el medio de la barra con la dirección indicada,
Saludos!
Lucía
Muchas gracias Lucia! se entendió perfecto.
