Ej de integrador
de Gomez Manuel - Buenas tardes,
Tengo dudas acerca de la resolucion del ejercicio que adjunto, es el T1.
Para la parte del desarrollo de f^(n) (i) pense en usar la formula integral de Cauchy (derivadas sucesivas), pero en el denominador me queda (z-i)^(n+1), con lo cual no encontre manera de relacionarlo con el dato del enunciado.
Saludos
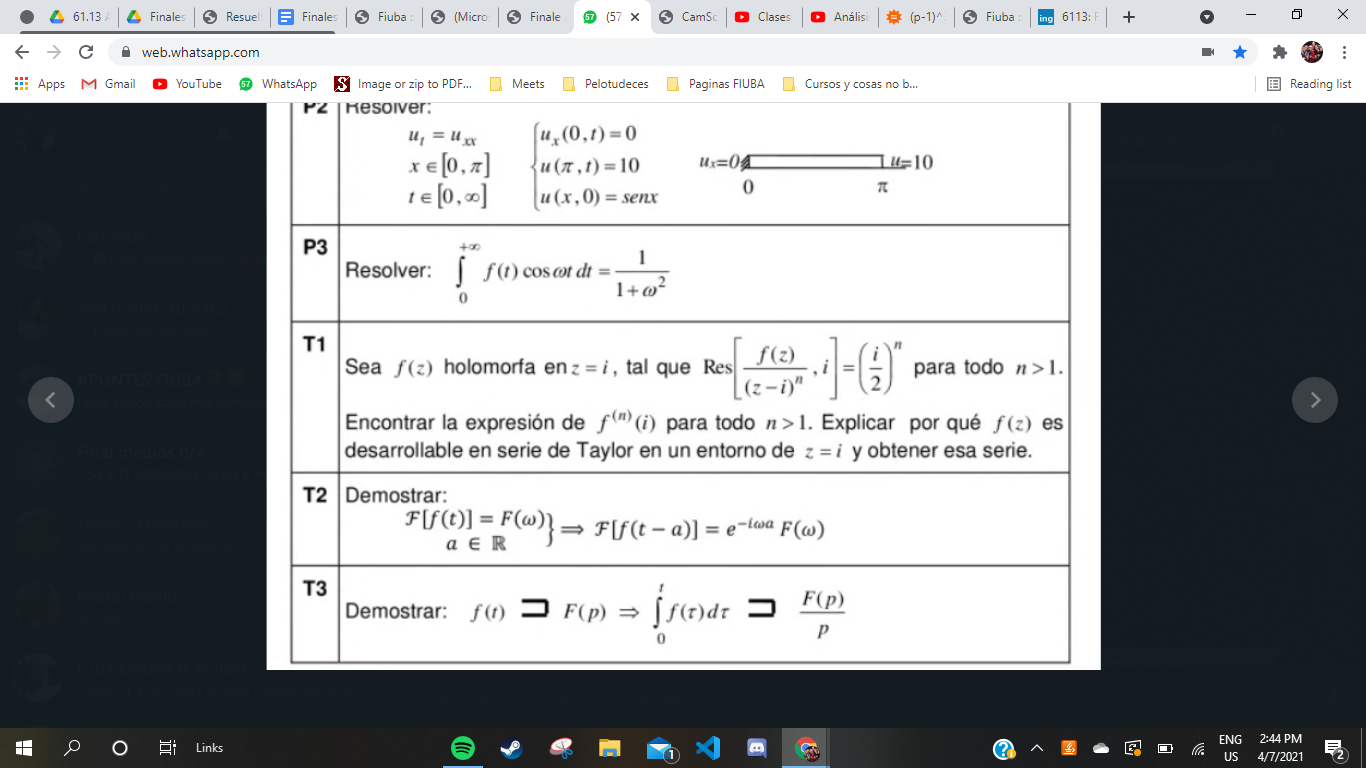
Re: Ej de integrador
de BARRERA SANCHEZ KELLY JOHANA - Hola Manuel,
El ejercicio no va por ese lado, es más sencillo de lo que parece.
Plantea el residuo para un polo de orden n en z=i de la función f(z)/(z-i)^n, es decir, plantea el limite con z-->i de (1/(n-1)!) * derivada de orden (n-1) de [(z-i)^n * f(z)/(z-i)^n]. Los (z-i)^n se te van a simplificar quedándote el límite de z-->i de (1/(n-1)!) * f^(n-1) (z) y esto por enunciado es igual a (i/2)^n.
Si aplicamos el límite va a quedar que: (1/(n-1)!) * f^(n-1) (i)=(i/2)^n.
Ahora como lo que se está pidiendo es la derivada de orden n y no de orden n-1 simplemente reemplaza n por n+1 y despejando te queda que f^(n) (i)=n!*(i/2)^(n+1).
Saludos.
El ejercicio no va por ese lado, es más sencillo de lo que parece.
Plantea el residuo para un polo de orden n en z=i de la función f(z)/(z-i)^n, es decir, plantea el limite con z-->i de (1/(n-1)!) * derivada de orden (n-1) de [(z-i)^n * f(z)/(z-i)^n]. Los (z-i)^n se te van a simplificar quedándote el límite de z-->i de (1/(n-1)!) * f^(n-1) (z) y esto por enunciado es igual a (i/2)^n.
Si aplicamos el límite va a quedar que: (1/(n-1)!) * f^(n-1) (i)=(i/2)^n.
Ahora como lo que se está pidiendo es la derivada de orden n y no de orden n-1 simplemente reemplaza n por n+1 y despejando te queda que f^(n) (i)=n!*(i/2)^(n+1).
Saludos.
Re: Ej de integrador
de Gomez Manuel - Buenismo Kelly, muchas gracias. Muy claro.
Saludos
