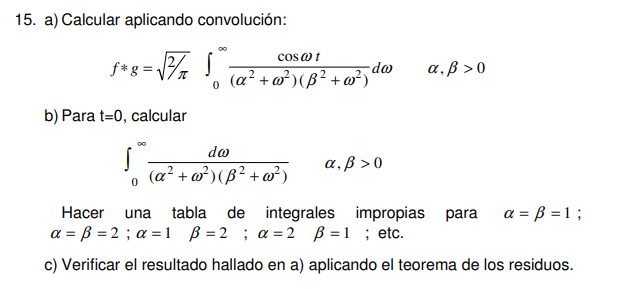
Estaba tratando de hacer este ejercicio. Hice la parte b y c, pero no logre entender como haría la parte a, ya que no estaría definido el producto de convolución y si la resolviese pasando a complejos, sería igual a la parte c. También pensé en verla como una antitransformada, pero no me sirvió de mucho.
Saludos, Agustín
Hola Agustín.
No estoy seguro a qué te referis con que el producto de convolución no está definido. La definición podes repasarla en el siguiente ejercicio resuelto de la guía: TP9-A12.
El punto a) entiendo que apunta a identificar que hay una función, que podemos llamar h(t), que es igual al producto de convolución de f y g. Además en el enunciado, se esta calculando esta función h(t) por medio de la antitransformada de Fourier.
Entonces lo que está adentro de la integral hay que pensarlo como la H(w) que es la transformada de Fourier de h(t). Por propiedad del producto de convolución, H(w) = F(w) G(w).
F(w) y G(w) tienen la misma expresión, solo difieren en el parametro alpha o beta, mientras que el cos(wt) es la parte real de la exponencial compleja en la expresión de la antitransformada. (También podría pensarse como antitransformada coseno, aunque la propiedad de la transformada de un producto de convolución creo que en la teórica solo fue demostrada para el caso de la Transformada de Fourier)
Como se puede observar que ambas funciones F y G son pares, la parte imaginaria de la integral (que contiene a sen(wt)) da cero y la parte real se puede calcular como 2 int_0^inf.
El ejercicio se reduce a identificar quién es f(t) (antitransformando F(w)), por similitud identificar g(t), y luego hacer el producto de convolución entre f y g, siguiendo la definición de producto de convolución.
En el punto b, es evaluar h(t) en t=0 para distintos casos de alpha y beta.
En el punto c entiendo que pide resolver la integral del punto a con los métodos de resolución de integrales impropias.
Saludos
Eso mismo es lo que termine pensando, el problema es que cuando tengo las antitransformadas se me complica el producto de convolución. Si tomo a F(w)=1/(w^2+a^2) la antitransformada queda f(t)=(pi*e^-a|t|)/a asumiendo que a es positivo y la otra es igual pero con b. Entonces cuando quiero hacer el producto me quedan módulos y condiciones que si las planteo no logro resolver la integral. Entonces no sabría como encararlo.
