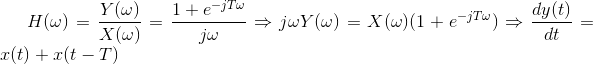Buenos días, pregunto por acá porque todavía está pendiente mi aceptación en el grupo de Google.

Estaba intentando representar un interpolador/retenedor de orden cero mediante ecuaciones diferenciales. La rta. al impulso del retenedor es:

h(t) = 1, 0<t<T

Por lo tanto, el sistema es LTI y causal  (porque la rta al impulso es cero para tiempos negativos). Por lo tanto puedo asegurar que puede representarse mediante una ecuación diferencial.

La transformada de Fourier de h(t) es:

H(w) = T sinc(wT/2pi)*exp(-jwT/2) = (2 sen (wT/2)/w)*exp(-jwT/2) = (1 - exp(-jwT)) /( jw) = (jw - jw *exp(-jwT)) / (jw)^2

Hasta ahí llegúe. ¡No logro poder representar H(w) como un cociente de polinomios en jw! ¿Es efectivamente posible hallar la representación que estoy buscando? ¡Gracias!