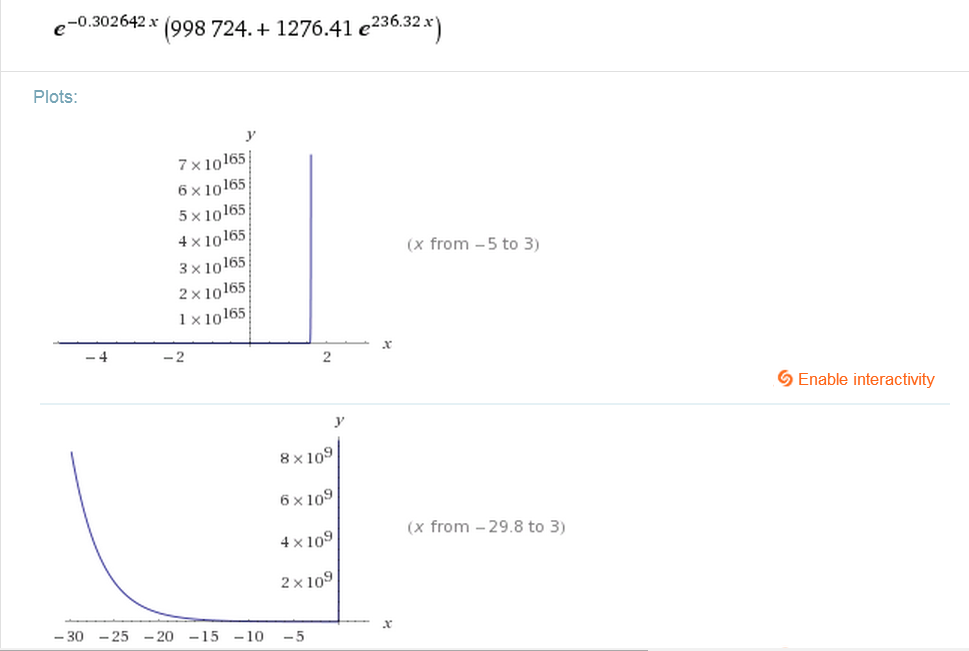
Buenas! Había consultado algo de esto en la clase de ayer, pero como había perdido las hojas de lo que hice no pudimos llegar a nada, así que pregunto por acá. Ayer quise resolver la ec. dif. del TP2 de forma analítica (con la solución como cl de exponenciales) para poder comparar los resultados del TP con el resultado verdadero, pero cuando lo hice llegué a que la solución tenía que ser una función que para x->infinito daba que era infinito (cosa absurda porque se trata de la concentración de ceniza en un problema de dispersión). La puse después en el wolfram para que la resuelva, y me dio de resultado lo mismo a lo que yo había llegado (dejo la imagen con el resultado ahí).
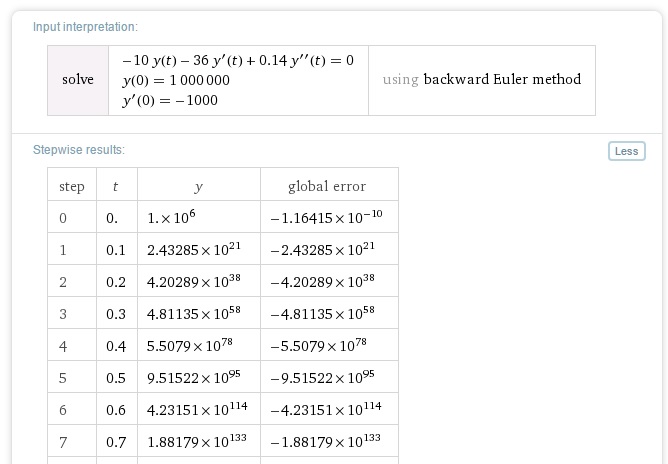
Por otro lado, cuando quise hacer el problema con Euler implícito, me quedó que la concentración de ceniza SI iba disminuyendo a medida que x aumentaba... ¿Puede ser entonces que la ecuación del TP no esté condicionando al problema como corresponde? Y si es así, no entiendo por qué Euler implícito me da que la cocentración tiende a 0... Dejo el screenshot de la solución del wolfram (la ec. dif. era 0,14y''-33y'-10y=0)
Buenas... La concntración tiene que tender a cero! a medida que me alejo del volcán las cenizas estan mas dispersas. A mi me dió que la condicion de C (x) < 0,1 mg/m3 se cumplió a 15896 km (me parece demasiado). Pero bueno.
Saludos. Yo estoy teniendo el mismo problema, cuando quise resolver la ecuación analíticamente para poder comparar luego me quedó que la concentración divergía a medida que x crecía (de hecho, crecía muy rápidamente, tanto que los valores se disparaban incluso para valores pequeños de x).
Resolviendo el sistema mediante el método de Euler explícito con distintos pasos también obtuve que la concentración divergía. Sin embargo, al probar con la versión implícita la concentración disminuía a medida que x crecía, tendiendo a 0. Con Euler implícito se cumplió la condición de la concentración menor a 0.1 mg/m^3 en aproximadamente 68 km. No obstante, la solución que arroja el wolfram al pedirle que resuelva el sistema con Euler implícito es que la concentración diverge (en la imagen).
Esto me trae dos interrogantes: si se supone que el método implícito aproxima a la solución real, no comprendo por qué obtengo resultados que se contradicen con la solución analítica (supongo que estaré empleando mal el método, pero lo revisé varias veces y no encuentro donde está la falla). ¿Es posible que el problema esté condicionado de manera tal que no sea viable aplicar Euler implícito?
En segundo lugar, y más allá de si estoy aplicando correctamente o no el método de Euler, la solución analítica indica que la concentración diverge, lo cual no concuerda con las características físicas del problema. Se me ocurre que quizás la ecuación dada no condiciona realmente un problema de difusión. No se si será eso, o si existirá más de una solución al sistema, pero no se me ocurren más cosas que probar.