Hola, nueva pregunta:

El punto «a)» lo hice sin problemas, encontré un teorema que apliqué y listo.
Para el punto «b)» lo que pedí es que el sistema tenga un cero en z=e^(j pi/3). El problema es que la transferencia es un "polinomio de grado N" de potencias negativas del cual no tengo idea cómo sacar las raíces. Asumiendo que fuesen potencias positivas, se sacar las raíces hata grado 2, grado 3 con Wolfram Alpha (que no tengo durante el examen), pero grado N es imposible.
Yo estuve viendo este problema tambien. Lo que se me ocurrio es que como pide el menor N que satisfasga lo pedido, tomo N = 6 de modo que muestrada la transformada Z en el circulo unitario se tenga para k = 1 z=e^(j pi/3). Entonces haciendo b1=0 se anularia la sinusoide de frecuencia pi/3. No se si habra una manera de anularla para un N menor...
Claro. Lo que no sabemos es si los ítems «a)», «b)» y «c)» se tienen que cumplir a la vez o por separado. Si se tienen que cumplir todos al mismo tiempo, no se nos ocurre bien cómo hacer, nos están quedando un montón de cuentas que no creo que halla que ponerse a hacer durante un examen. Si se tienen que cumplir por separado es más fácil.
Hola, el punto b) implica que la transformada Z de tu filtro tiene que anularse para z=exp(j pi/3) y también para z=exp(-j pi/3). Esto lo lográs con el siguiente término multiplicativo:
(1 - z^-1 exp(-j pi/3)) . (1 - z^-1 exp(j pi/3))
Si lo desarrollás tiene orden 2. Si la TZ tiene otros requisitos, este término multiplicará al resto, incrementando el orden del sistema.
Saludos
Luego de un largo debate y pruebas, llegamos a la conclusión de que es clave hacer dibujos. Resolvimos el ejercicio cumpliendo todas las condiciones haciendo el diagrama de polos y ceros (en realidad, de ceros) de lo que buscamos
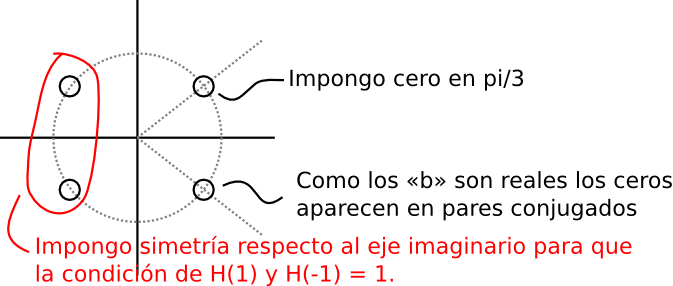
Lo primero que hicimos fue poner un cero en pi/3 para el punto «b)». Como el filtro tiene que tener coeficientes reales (por el punto «a)»), entonces automáticamente hay que poner el cero complejo conjugado.
Para cumplir con el punto «c)» lo que dijimos fue "bueno, ya que las condiciones se imponene para z=1 y z=-1, hagamos que sea simétrico y listo, es más fácil".
Pidiendo esto nos quedó H(z) = 1/3 * (z⁴ + z² +1) ❤
Me surgen un par de preguntas sobre el planteo.
¿Porque completar con 2 ceros en el semieje real negativo hace que se cumpla la condición H(1)=H(-1)=1?
¿De donde sale el 1/3 de la expresión final? desarrollando el producto de todos los ceros me queda la misma expresión pero sin el 1/3.
Lo de agregar 2 ceros es porque hace que la función sea simétrica con respecto al eje imaginario, entonces si hacés que H(1) = 1 automáticamente H(-1) = 1.
El 1/3 es para ajustar que H(1) = 1.
