(Editado por Zhao Yuchen - envío original Monday, 29 de June de 2020, 18:48)
Sí (si es diagonalizable), si hablando del TP4.
Buenos días.
me pareció muy interesante la pregunta que Siguenza planteó en el foro : ¿debería un sistema representado en sus tres formas canónicas (Controlable, Observable y Diagonal) tener la misma respuesta en régimen libre para un mismo estado inicial x0?.
Creo que se justifica trabajarla con algún detalle para aclarar conceptos.Por eso les propongo, a todos, este ejercicio:
Definamos una transferencia para ser estudiada, G(s). Podría ser un sistema definido por tres bloques, G1(s), G2(s), G3(s) de modo que G(s)= G1(s).G2(s).G3(s) .
Para que el problema sea interesante no todos los polos deberían ser reales, por supuesto, y debería tener algún/os cero/s. Para no complicarlo mucho, sugiero que G(s) sea de un sistema estable.
Les propongo que dos de uds. (por ejemplo, Andrada y Ross, )
*) definan la G(s) a estudiar y nos lo informen a todo el curso. También, la amplitud de un escalón de entrada y el valor de la condición inicial en régimen libre.
Luego:
*) hagan un diagrama de flujo de señal, considerando que x1 es la salida de G1, x2 es la salida de G2, x3 es la salida de G3.
*) planteen el modelo de variables de estado
*) simulen la respuesta del sistema a la señal de entrada
*)simulen la respuesta del sistema a la condición inicial
Simultáneamente, que
otros participantes del grupo (por ejemplo, Quevedo Meza, Diego Rojas, Barcenas Arias )
*) lleven el sistema a forma canónica de controlador
*) hagan un diagrama de flujo de señal, eligiendo la salida de los bloques integrador como x1c, x2c, x3c
*) planteen el modelo de variables de estado
*) simulen la respuesta del sistema a la señal de entrada
*) simulen la respuesta del sistema a la condición inicial
otros participantes del grupo (por ejemplo, Driden Urbano, Vasquez Salis, )
*) lleven el sistema a forma canónica de observador
*) hagan un diagrama de flujo de señal, eligiendo la salida de los bloques integrador como x1o, x2o, x3o
*) planteen el modelo de variables de estado
*) simulen la respuesta del sistema a la señal de entrada
*) simulen la respuesta del sistema a la condición inicial
otros participantes del grupo (por ejemplo, Ramirez Granja, Reginaldo Quispe, Siguenza Barros )
*) lleven el sistema a forma canónica modal
*) hagan un diagrama de flujo de señal, eligiendo la salida de los bloques integrador como x1*, x2*, x3*
*) planteen el modelo de variables de estado
*)
simulen la respuesta del sistema a la señal de entrada
*) simulen la respuesta del sistema a la condición inicial
Cuando tengamos esto finalizado, compararemos los resultados para sacar conclusiones y aclarar las dificultades conceptuales que se nos puedan haber presentado en la resolución.
Sugiero hacer el trabajo con la mayor claridad y prolijidad posible para facilitar la comparación entre los resultados particulares.
Propongo la siguientes transferencias para que comencemos a trabajar.
Con escalón de amplitud 1.
Saludos,
Va de nuevo porque no me lo tomo.
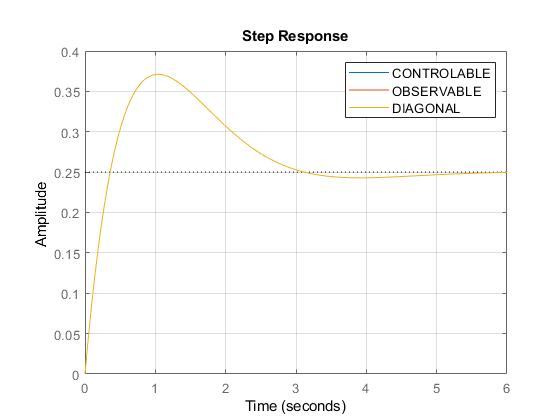
Efectivamente, al realizar la respuesta al escalón del sistema G(s) propuesto por ROSS en sus 3 formas canónicas (Controlable, Observable y Diagonal) se observa que generan exactamente la misma respuesta.
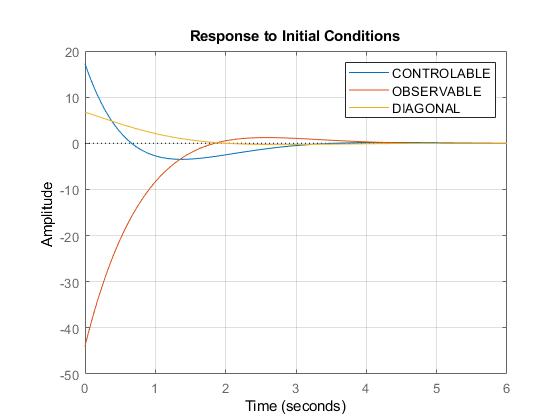
Sin embargo, la respuesta en régimen libre ante un estado inicial x0 son diferentes, pienso que esto es debido porque la respuesta depende solo de la matriz A y C y no de la B ya que u=0. Al ser las matices A, B y C diferentes entre si de todas sus forma canónicas (Controlable, Observable y Diagonal) para el mismo sistema, la respuesta en estado inicial es diferente.
Entonces, hago las siguientes preguntas:
¿Por qué las 3 formas canónicas dan la misma respuesta al escalón de entrada a pesar de que sus matrices A, B y C son distintas?
¿Qué debería hacer para que las 3 formas canónicas tengan la misma respuesta en régimen libre, ya que dichas formas representan el mismo sistema?
Hola.
Ahí dejo los ejercicios del sistema G(s) propuesto por ROSS en su forma original y comparado a sus 3 formas canónicas (Controlable, Observable y Diagonal) para las condiciones iniciales propuestas.
(Revisar documento).
En base a los comentarios de Vasquez, se comprueba que al multiplicar el vector de estados iniciales por la matriz de transformación de cada forma canónica, se obtiene la misma respuesta en estado inicial.
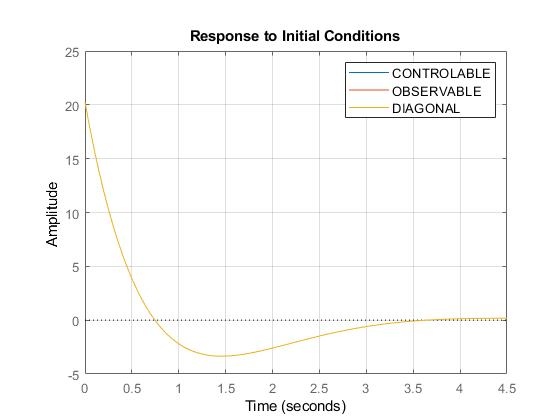
Se concluye que cada forma canónica (Controlable, Observable y Diagonal) contiene su matriz de transformación T referente al sistema original. La respuesta en estado inicial es diferente en cada caso, debido a que depende de la dinámica solo de las matrices A y C, la multiplicación del vector de el vector de estados iniciales por la matriz de transformación de cada forma canónica, se obtiene la misma respuesta en estado inicial. Mientras que la respuesta al escalón es la misma para cada caso, esto debido a que depende de la dinámica de todas sus matrices (A, B, C y D).
Buenas ,
subo mi parte del sistema G(s) propuesto por ROSS en la forma canónica de controlador y sus respuestas ante una señal de entrada y también para sus condiciones iniciales xo.
Saludos,
Estimados, buenas noches.
Con respecto a lo propuesto por el Sr. Ross, con mi análisis, creo que la función de transferencia en sus tres formas canónicas con una condición inicial, no tienden a una misma respuesta.
añadiendo a esto, tengo una duda, al representar la forma canónica diagonal, la función transferencia debe ser descompuesta en fracciones parciales, tanto numeradores y denominadores de estas, tienen raíces imaginarias, y como podría representar esto en diagramas de flujo de señal?, o no es posible?.
Saludos.
Añado un análisis de cada una de las formas canónicas con respecto a la función de transferencia original, ante condiciones iniciales nulas, condiciones iniciales planteadas y condiciones iniciales adaptadas.