Publicar en ese hilo cualquier consulta relacionada con la Unidad 8
Hola, el video b de las clases practica esta en privado. No se si es a proposito o por un error, pero aviso por las dudas
Gracias por avisar.
Ese video es la explicación del trabajo práctico del cuatrimestre anterior. Por eso lo sacamos de circulación.
Buenas, estoy realizando la guía 8 y en un par de ejercicios me piden utilizar el método de Crank-Nicholson. Con este metodo me surge una duda.
El método de Crank-Nicholson viene dado por la siguiente expresión
u(n+1) = u(n) + h/2 * ( F( u(n+1), t(n+1)) + F(u(n), t(n)))
Donde (n) son los índices.
Mí duda surge con el u(n+1) ya que está en adelanto y no sé cómo calcularlo.
Saludos.
Hola Federico.
Hay dos maneras de hacerlo.
1- La más rigurosa, es plantear la ecuación directamente, de manera que u(n+1) queda tanto en el lado iquierdo como derecho de la ecuación. Por lo tanto queda definido un problema de raices en cada paso de tiempo, y hay que usar alguno de los métodos conocidos para calcular u(n+1). Por ejemplo usando Newton-Raphson.
2- Otra forma es utilizar un método explícito, como por ejemplo Euler, para calcular un valor aproximado de u(n+1). Luego aplicar Crank-Nicholson usando ese valor estimado del lado derecho para calcular un valor más preciso del lado izquierdo.
Saludos.
Hola, en el minuto 4:50 del video P08e - Problemas de Valores de Contorno (PVC), quería saber como salen los resultados de u(1)=0,815 y u(1)=1,222, ya que si uno reemplaza en la ecuación de u(n+1) que se obtuvo, los valores de v(0)= 20 y v(0)=30, no dan los resultados de u(1)= 0,815 y u(1)=1,222.
Desde ya muchas gracias
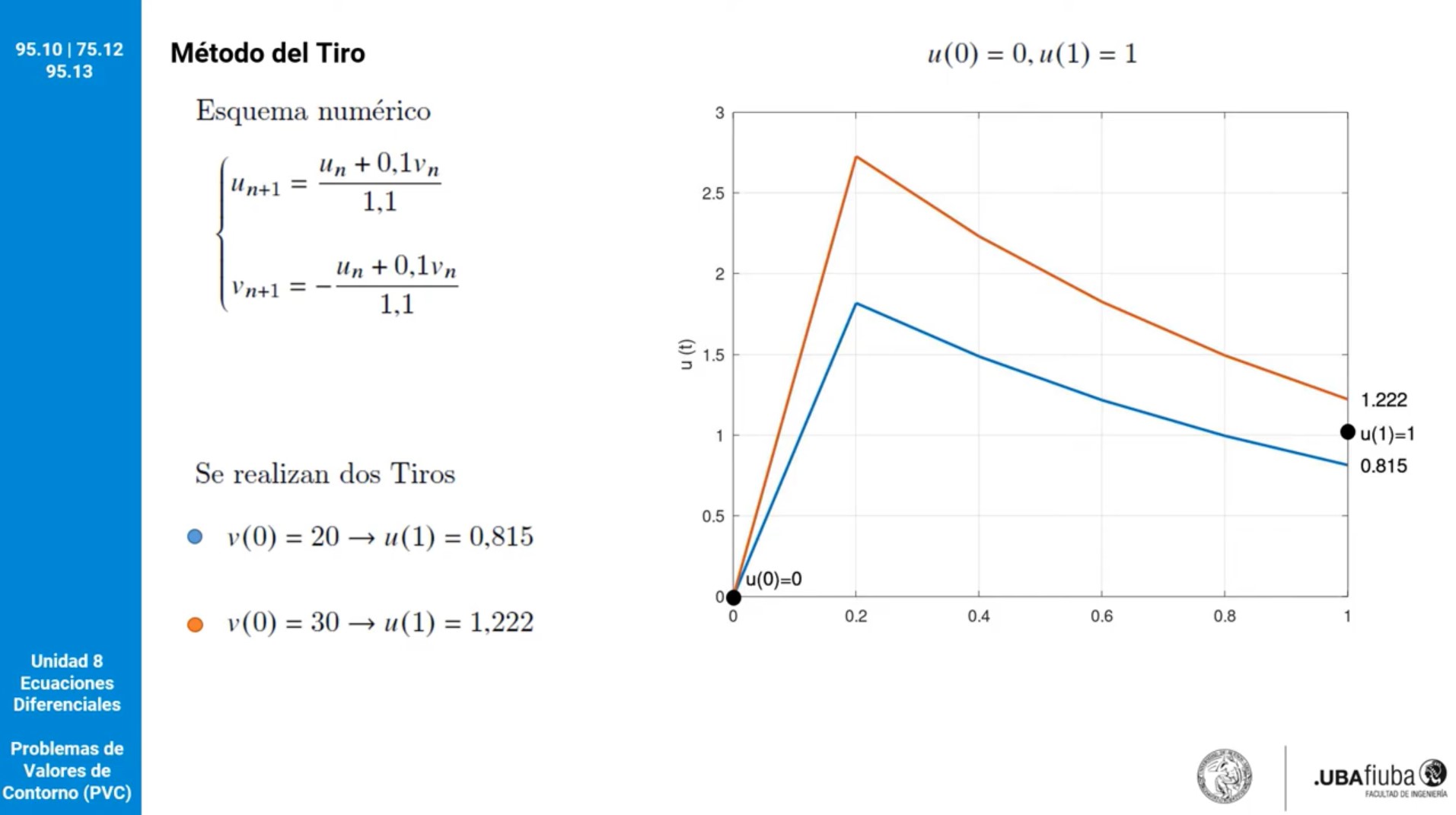
Hola Juan,
En el método de tiro se asumen condiciones iniciales (en este caso en t=0), y se resuelve el PVI hasta llegar al otro extremo (en este caso t=1), para ver si los valores asumidos son correctos.
Esa resolución consta de un cierto número de pasos, en general mucho mayor a 1. En este caso el paso de cálculo es h=0.2, por lo cual se deben realizar 5 pasos para llegar de t=0 a t=1. Es decir, tenés que aplicar la fórmulas 5 veces, no una sola.
Saludos
Buenas tardes, estaba realizando el ejercicio 2 de la guía 8. Llegue a que el factor de amplificación es el siguiente:
g = 1 + 2*k*u(n)
Ahora bien no estoy muy seguro de como analizar las condiciones que da el enunciado. Para el primer caso
u(0) > 0 y t0 < t < 1/u0
pensé que como u(0) es mayor a 0 el modulo del factor va a ser mayor a 1 en ese caso porque k también es mayor a 0. Luego como u(n+1) = un + k * (u(n))^2 todos los siguientes u(n) serán también mayores a 0. Pero no se si esta bien dado que no estoy teniendo en cuenta la otra condición.
Luego para el segundo caso
u(0) < 0 y 1/u0 < t0 < t
lo que pensé para el anterior entiendo que no tiene validez por el signo de u(n) y estoy perdido en como resolverlo. Tampoco se como usar la otra condición
Desde ya gracias,
Saludos
obtenidos o tenemos que interpolar los datos? Porque si trato de aplicarlo sobre los resultados obtenidos y por ejemplo el paso que me toca es 
, puede no se encuentre ese paso en mi tabla con su respectivo resultado , por eso pensé que quizás habría que interpolar para calcular valores intermedios.Buenas, estoy realizando ejercicios de sistemas de ecuaciones diferenciales y me surgió una duda respecto al método runge kutta 2
Supongamos que tengo las siguientes ecuaciones:
X' = 4x + 2y
Y' = -x + y
paso a variables discretas
x = s
y = w
F1 = 4s + 2w
F2 = -s + w
Aplico runge kutta 2
Sn+1** = sn + k * F1(sn,wn,tn)
Wn+1** = wn + k * F2(sn,wn,tn)
Sn+1 = sn + k/2 * [F1(sn, wn, tn) + F1(sn+1**, wn+1**, tn+1)]
Wn+1 = wn + k/2 * [F2(sn, wn, tn) + F2(sn+1**, wn+1**, tn+1)]
Mi duda es con la expresión en rojo( F2(sn+1**, wn+1**, tn+1) ) en Wn+1 ya que no se si usar la aproximación por Euler Sn+1** o la aproximación refinada Sn+1.
Es decir tengo que usar: F2(sn+1**, wn+1**, tn+1) o F2(sn+1, wn+1**, tn+1)
Desde ya muchas gracias.
Hola Federico; es como lo escribiste primero:
Sn+1 = sn + k/2 * [F1(sn, wn, tn) + F1(sn+1**, wn+1**, tn+1)]
Wn+1 = wn + k/2 * [F2(sn, wn, tn) + F2(sn+1**, wn+1**, tn+1)]
Saludos!Mis dudas son: ¿Es el método del tiro un método directo?
¿ Es el método de las diferenciasa finitas un método directo?.
En caso de que los anteriores métodos no fueran directos cual método tendria que usar ?
Saludos.
