Publicar en ese hilo cualquier consulta relacionada con la Unidad 3
Hola, buenas tardes.
En el ejercicio 13 de la guía se habla de "Efectuar las modificaciones necesarias para garantizar la convergencia" refiriéndose a la resolución mediante el método de Jacobi.
¿Cuáles podrían ser estas modificaciones?
Saludos, Tomás Fernandez.
Básicamente podés garantizar la convergencia con solo intercambiar las filas del sistema, porque entonces la matriz queda estrictamente diagonal dominante.
Saludos!
Perfecto! Gracias!!
ok
Hola! Se me esta complicando ver como definir la matriz p que de cuenta del pivoteo, pues en el ejercicio resuelto como ejemplo en youtube la matriz es 2x2, de modo que el cambio es evidente, pero en ejercicios como el 3.5 esto me genera mas problemas.
Adjunto mi resolución, hice dos pivoteos: en el primer paso intercambié la fila F2 con la F1, y en el segundo paso intercambie la "nueva" F2 con la F3. No veo como armar p. Ademas, cuando realizo L*U para verificar, obtengo una matriz que no es A con las filas intercambiadas como yo creería, pero los resultados numéricos de x1, x2, x3 me dieron bien así que no veo donde puede hallarse el error.
Desde ya muchas gracias!
Es muy sencillo. Al comenzar el ejercicio te escribís la matriz identidad:
o el vector
Luego durante el proceso de descomposición LU, cada vez que intercambias filas haces el mismo intercambio en la matriz o el vector
.
Es decir, no se arman al final, sino al principio, y se le van aplicando los cambios a medida que suceden.
Saludos
Una cosa más: acordate que tenés que pivotear también L junto con U y P. Para simplificar el proceso conviene hacer como explicamos en clase: escribir los multiplicadores en la propia matriz U.
Gracias! O sea que en este caso, p={2, 3, 1}?
Y yo pensaba usar que 
, buscar el residuo como 
, despues realizar la susutcion simple 
y por ultimo la sustitución inversa 
, de modo que obtengo el error de redondeo. En este caso no me conviene tener U y L separados así como los puse en el ej? (pregunto por tu segundo comentario)
Buenas tardes,
Me quedó una duda de la guía 3. En el ejercicio 5), por ejemplo, pide una "estimación del error de redondeo, refinando la solución.", no termino de entender qué es lo que me pide, ¿Sería el número de condición 
y la cantidad de dígitos que gano en cada refinamiento 
?
El enunciado dice:
5) Resolver el siguiente sistema:
![\left[ \begin{matrix}
2.15 & -0.924 & -1.29 \\
-4.12 & 2.29 & 0.294 \\
1.01 & 0.872 & -3.25
\end{matrix} \right] \cdot
\begin{bmatrix} x_{1} \\ x_{2} \\ x_{3} \end{bmatrix}
=
\begin{bmatrix} 1.22 \\ -3.56 \\ -0.972 \end{bmatrix}](https://campusold.fi.uba.ar/filter/tex/pix.php/5af02bba8b111268cd3c837e13cc4d55.svg "\left[ \begin{matrix}
2.15 & -0.924 & -1.29 \\
-4.12 & 2.29 & 0.294 \\
1.01 & 0.872 & -3.25
\end{matrix} \right] \cdot
\begin{bmatrix} x_{1} \\ x_{2} \\ x_{3} \end{bmatrix}
=
\begin{bmatrix} 1.22 \\ -3.56 \\ -0.972 \end{bmatrix}")
Utilizar eliminación de Gauss con pivoteo parcial. Hallar la descomposición LU de la matriz de coeficientes y utilizarla para hallar una estimación del error de redondeo, refinando la solución. Utilizar aritmética de punto flotante con 3 dígitos.
La diferencia entre las dos soluciones del sistema, la original y la refinada, te permite estimar el error de representación (que es la única fuente de error en este problema).
Buenos dias. Estaba realizando el ejercicio 5 de la guia y no logro identificar donde está el error. Me guie con el ejercicio Nº6 de la practica pero llego a un resultado erroneo. Quisiera saber si hay algun error conceptual en los diferentes pasos realizados y que eso lleve al resultado equivocado. Desde ya muchas gracias
Pareciera que el residuo r te da muy grande. La solución aproximada no te da tan lejos de la exacta.
Una pregunta, por qué en la clase del resuelto del ejercicio 6 al buscar el segundo refinamiento de usa la matriz A sin pivote a diferencia del primero?
Y otra duda que tengo es sobre la precisión. Veo que, por ejemplo si tengo el número 1,4341x10-3 y debo utilizar precisión 3, a veces aparece como 1,43x10-3 y otras como 0,001. Depende que uso dan valores muy distintos de residuales o valores estimados. ¿Qué forma es la correcta?
En el ejercicio 6, para el cálculo de residuo deben trabajar con las matrices permutadas, hay algún error en la presentación.
En el refinamiento 1, usando:
P.b = 1.89
1.62
P.A.x = 1.8926
1.61785
Entonces
P.r = P.b - P.A.x
P.r = -0.0026
0.00215
Luego L.E = P.r
U.Dx = E
L.E = -0.0026
0.00215
y del segundo sistema despejan Dx, si siguen la misma lógica obtienen el segundo refinamiento.
Respecto de la precisión, depende de lo que te diga el enunciado, en el ejemplo que presentas:
Si te dicen utilizar precisión 3, deberías utilizar 3 dígitos significativos, entonces te quedaría 1,43x10-3 o 0.00143. En general en la materia trabajamos con esto.
Pero en algunos casos en particular te pueden decir utilizar 3 decimales, en este caso sería 0,001. Pero no es lo más convencional.
Hola, quería consultar si hay algún resuelto del ejercicio 10
No hay resuelto del ejercicio10.
Hola, en el ejercicio 13 cuando me dice "Efectuar las modificaciones necesarias para garantizar la convergencia" que es lo que puedo modificar del problema? la matriz?
Porque viendo el radio espectral los autovalores de la matriz de iteración me dan imaginarios, y la norma muy grande. Lo único que se me ocurre es cambiar la matriz diagonal D para que la norma sea < 1 y también los autovalores me den reales y menores a 1.
El cambio que yo hice fue hacer que la nueva D sea igual a la inversa de la D anterior, y cambio un signo de un coeficiente para que los avals me den reales.
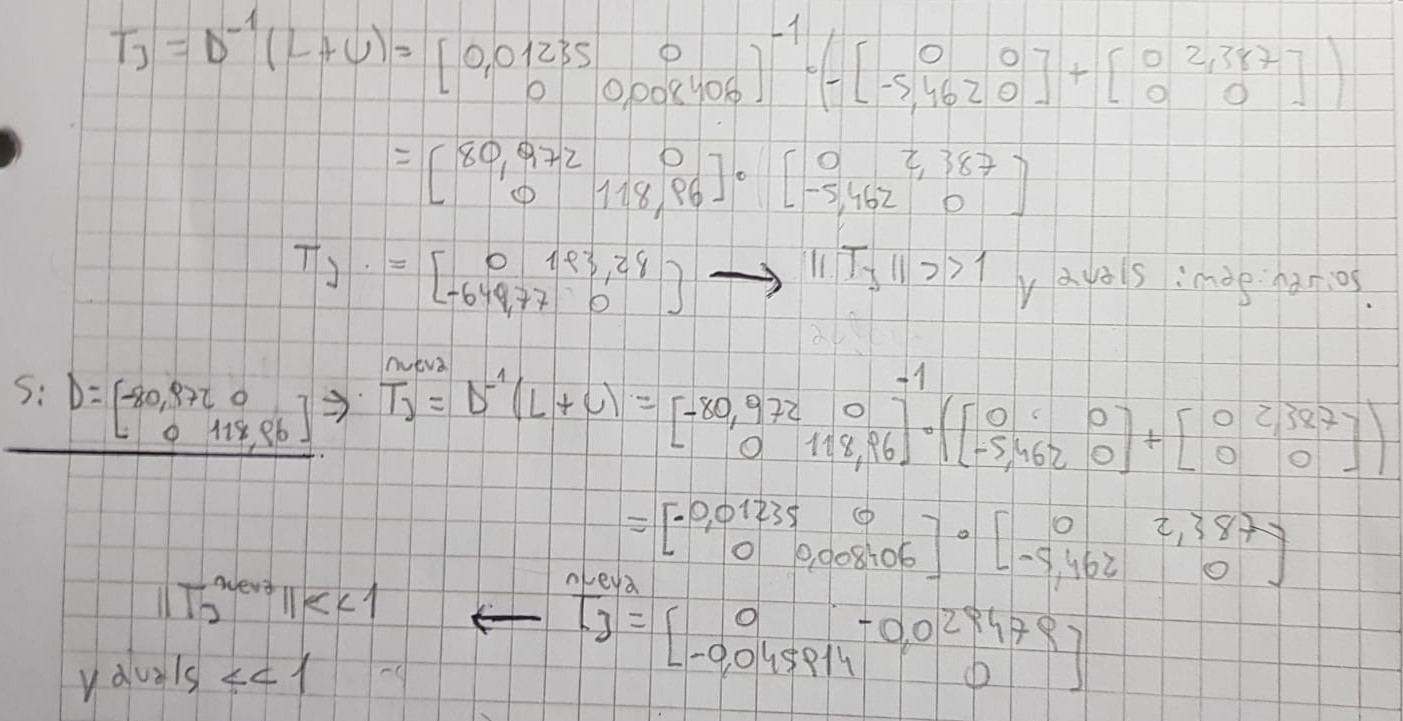
En el ejercicio 13, para garantizar la convergencia, podés pivotear las filas de la matriz A. De manera tal que en la diagonal te queden los valores mayores.