Buenas tardes, estoy teniendo complicaciones al momento de calcular la convergencia de la función que plantea el ejercicio en un V(∞).
Quise plantear el criterio de Abel, pero si llamo α(x)=1/(a^2-x^2) la misma no cumple ser α(x)>0 ni α´(x)<0 para valores de x ϵ (a, ∞).
Si hay algún otro camino o estoy teniendo un error, me sería de gran ayuda saberlo.
Muchas gracias!
Tené en cuenta que podes combinar criterios. Por ejemplo en este caso podrías como primer paso mayorar el integrando cambiando cos(x) por 1 (que en valor absoluto es mayor o igual), y luego comprar por paso al límite con 1/x^2.
Podrías así demostrar la CV absoluta en V(inf). Tené en cuenta que además tenés que ver las raíces del denominador. Al ser polos simples no hay convergencia, aunque si existe valor principal.
Perfecto Julián! Muchas gracias. Sería algo así? La única duda que me queda es que para dividir por (a^2 - x^2) tengo que pedir que sea mayor a cero, por lo tanto valdría para los a>x. Es correcto o me estoy mareando?
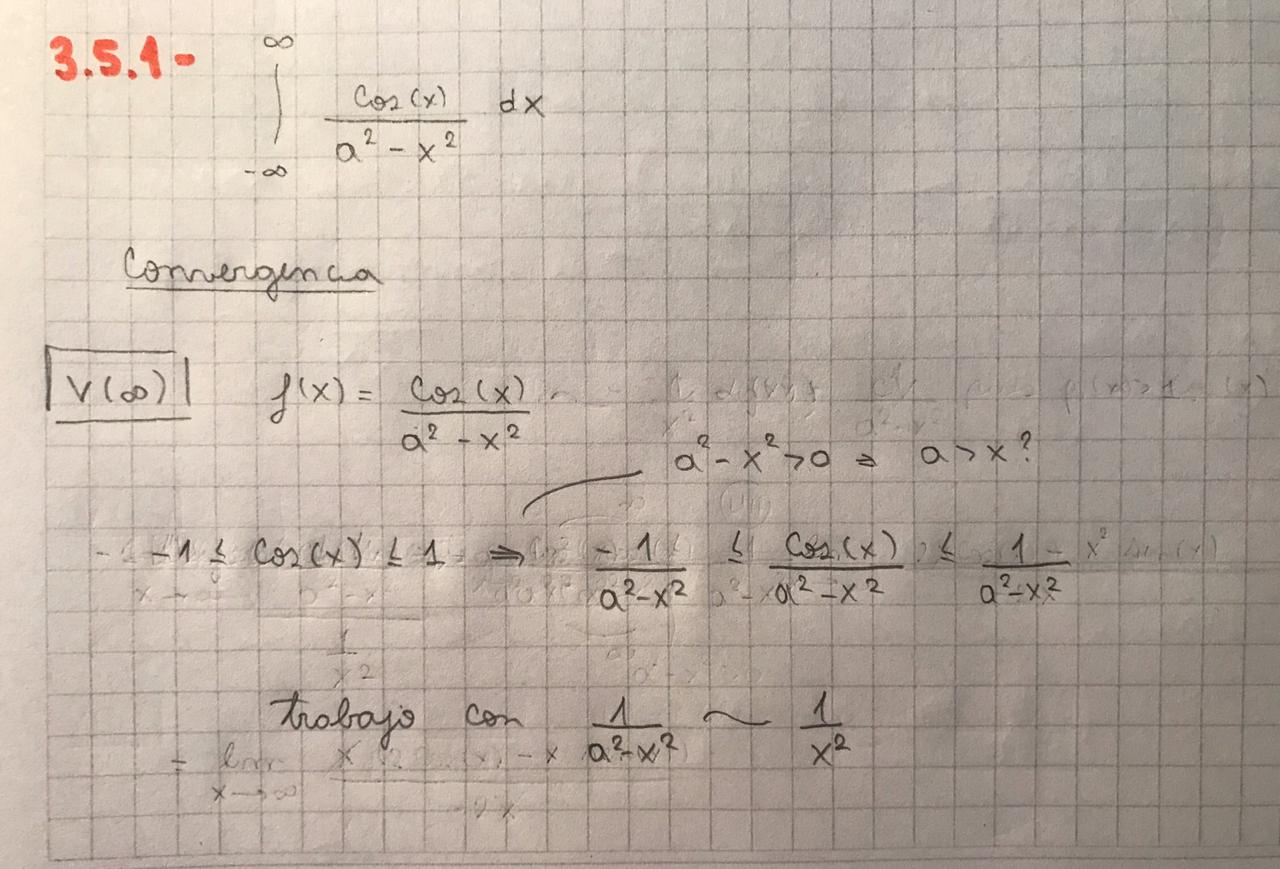
Si, es un poco más fácil. Lo primero que podrías hacer es aplicar módulo a f(x), tanto numerador como denominador. Si estás analizando el vecinal de infinito, el módulo del denominador es x^2-a^2. El numerador es menor o igual a 1, por lo que te queda |f(x)|<=1/(x^2-a^2). Si tomás límite cuando x tiende a infinito de |f(x)|/|g(x)| con g(x)=1/x^2 demostrás la CV absulota en V(inf)...
La cuenta que hiciste no vale para V(inf), que es lo que estás analizando, porque allí es negativo el denominador a^2-x^2. Recordá que cuando multiplicas o dividís una desigualdad por un número negativo, se deben invertir los signos de <, <=, etc.
Acordate que en x=a y x=-a no hay CV en casi todos los valores de a, pero si valor principal, por lo que la CV absoluta en V(inf) no se translada a la integral total que diverge pero tiene valor principal.
Los casos particulares son cuando a es tal que cos(a)=0. Ahí la CV mejora.
Muchas gracias!
