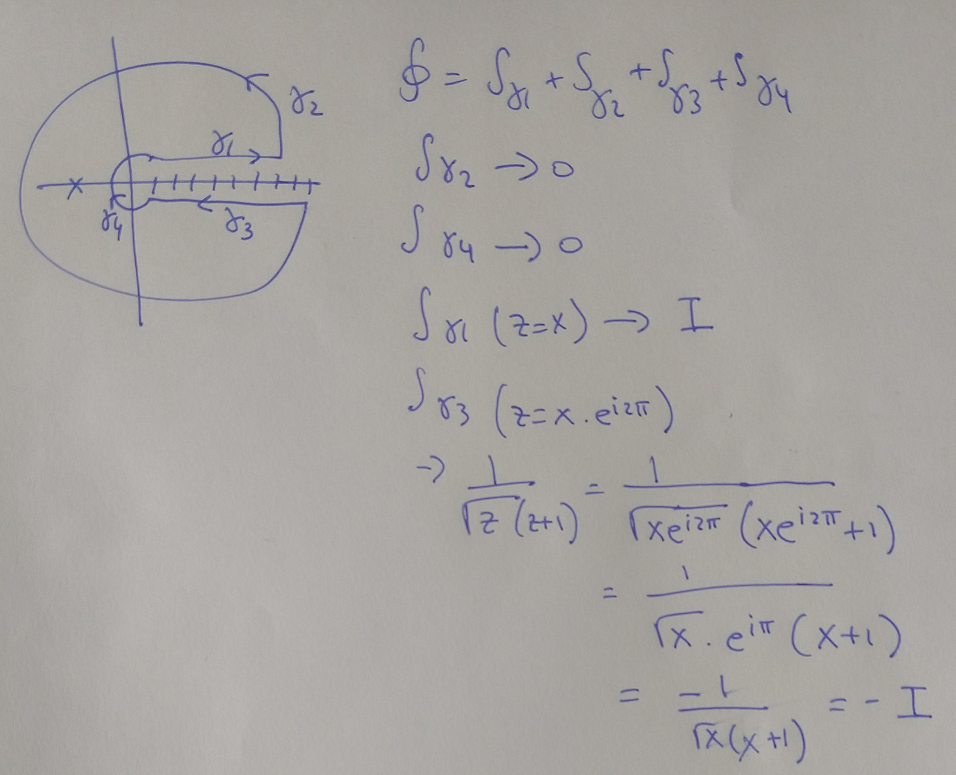Buenas tardes,
Tengo una duda con el ejercicio que adjunto.
Ya analice la convergencia de la integral, pero a la hora de calcular el valor principal no se si estoy haciendo las cosas bien. Pensé en armar un arco de circunferencia "saltando" las singularidades, pero el integrando es desde 0 a + infinito, con lo cual me parereció incorrecto. Seria valido tomar un arco que barra de 0 a pi/2 ?
Saludos
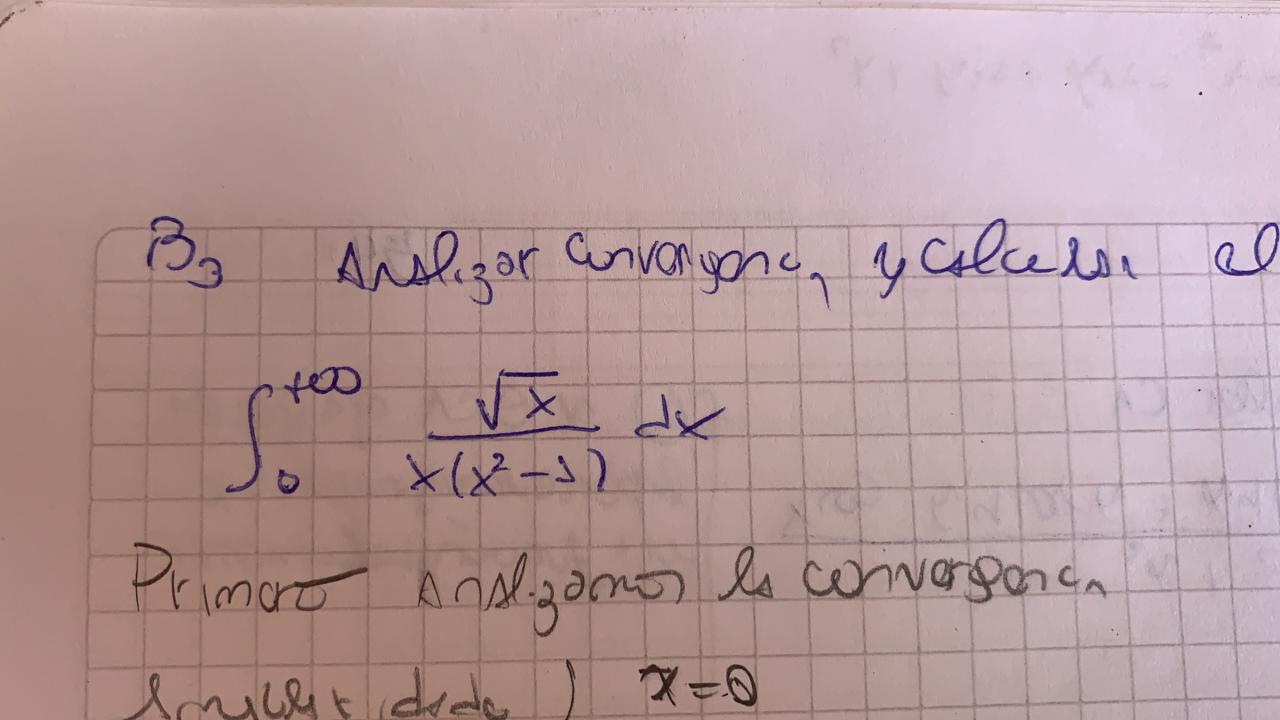
Hola Manuel,
Para el cálculo del valor principal de la integral, al pasar de x a z, te va quedar que f(z) tiene singularidades en z=1, z=-1 y z=0 donde esta última al haber una raíz(z) tendremos que z=0 es punto de ramificación, por lo que vas a tener que hacer una cortadura para uniformizar esa función.
El camino que mencionas, una semicircunferencia de radio R saltando las singularidades es un posible camino, no importa que la integral que te piden vaya de 0 a +infinito, luego cuando operes vas a poder pasar de la integral de -inf a +inf a una integral de 0 a +inf.
Te recomiendo que mires los videos 20 y 21 del TP 5 que son casos en donde se tienen puntos de ramificación, los links son los siguientes:
https://www.youtube.com/watch?v=KhOUDaGXj3Q&list=PLXqoZ7Eo4b4s3Cob1oQNyCSiwQcJ2_Lj3&index=20&ab_channel=An%C3%A1lisisMatem%C3%A1ticoIII-Murmis
https://www.youtube.com/watch?v=KJAX7vRanZs&list=PLXqoZ7Eo4b4s3Cob1oQNyCSiwQcJ2_Lj3&index=21&ab_channel=An%C3%A1lisisMatem%C3%A1ticoIII-Murmis
Te adjunto foto del posible camino de integración.
Perfecto, muchas gracias. Ahora intento resolverlo, y si no es molestia, adjunto el desarrollo para comprobar que sea correcto.
Saludos
Si fuese así, una integral me queda con el integrando de -1 a infinito.
Lo otro que se me ocurrió, fue aplicar el teorema de la integral que rodea a un polo simple.
Cual es correcta?
Saludos
Las integrales de los segmentos entre singularidades no tienes que resolverlas como tal, la suma de las cuatro integrales que están sobre el eje x cuando r tienda a 0 y R tienda a inf te da que esa suma tiende a la integral desde -inf a +inf (r es el radio de la semicircunferencia que rodea a las singularidades y R es el radio de la semicircunferencia grande).
La integral de la semicircunferencia de radio R da cero y lo justificas con el Teorema de acotación de un arco de Rinf, las que tienes que resolver aplicando teoremas son las integrales que rodean a las singularidades.
Saludos.
Impecable Kelly, lo pude resolver. Muchísimas gracias. Me quedo una duda, no afecta en mucho a la resolución, pero para saber. En este caso, z=0 es pto de ramificación y polo, es necesario calcular su residuo o modifico la expresión poniendo la raíz en el denominado, de tal manera que z=0 (si no me equivoco) sea solo pto de ramificación?
Perfecto, de nuevo, muchísimas gracias. Saludos
Buenas, me surgió una consulta sobre un ejercicio de parcial similar así que aprovecho la publicación.
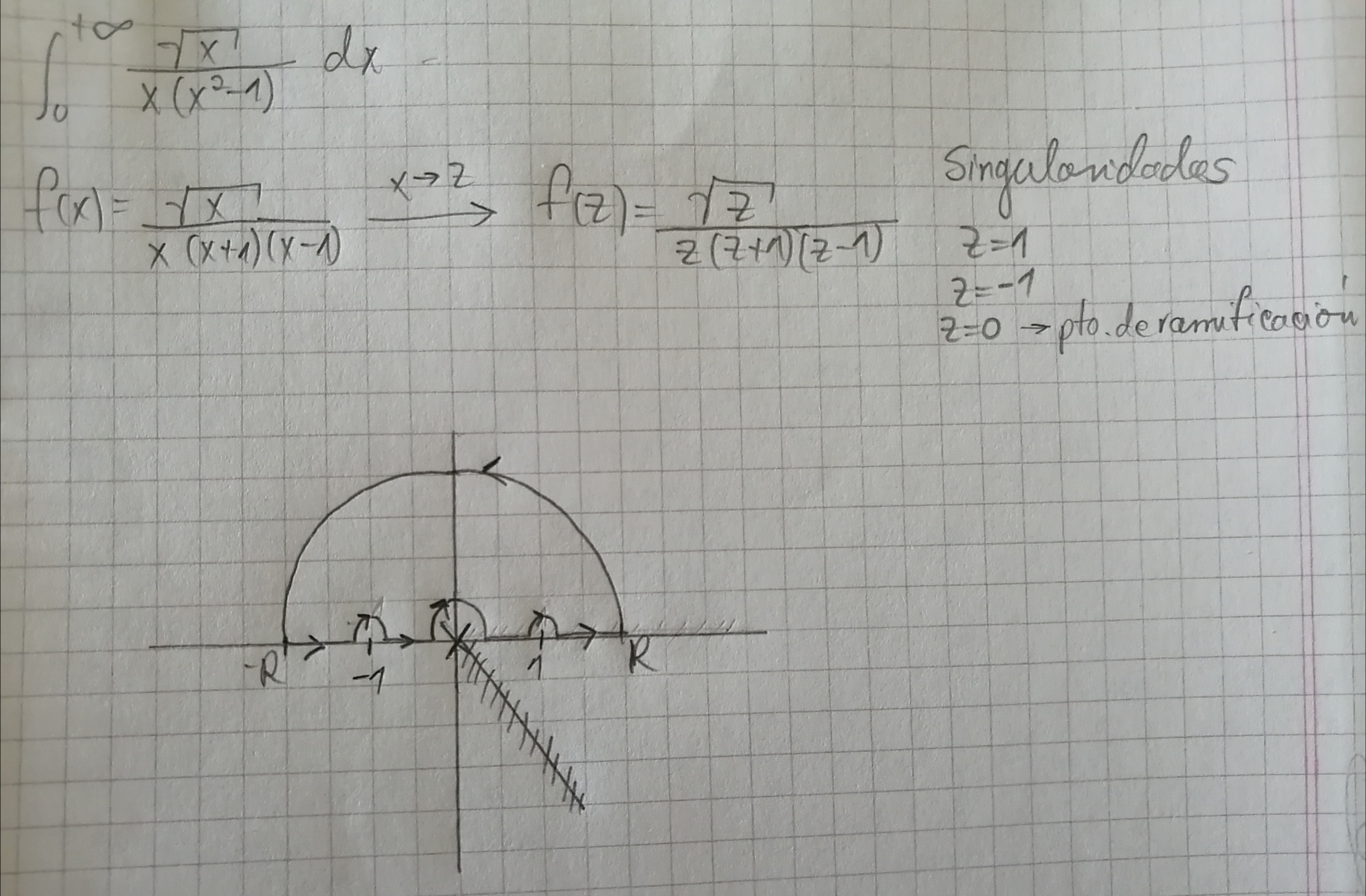
En el caso que adjunto más abajo planteo un camino de integración similar al que plantearon en el ejercicio anterior, pero no estoy seguro sobre cómo analizar z=0 donde está el punto de ramificación. Si multiplico f(z) por raiz de z y tomo límite con z → 0 me da 0. Entonces resulta que no es polo simple. Ahora bien, para calcular la integral que nombro como "5", se puede usar el teorema de acotación de un arco de radio 0 para decir que la misma termina valiendo 0?
Luego cuando obtengo de 2, 4 y 6 la integral desde -∞ a +∞ (tal como explicó Kelly antes), cómo puedo hacer para llevarla a los límites que pide el enunciado que son de 0 a +∞? Como hay una raíz que no es una función par ni impar supongo que no puedo encarar por este lado.
Espero haber sido claro, gracias.

Buenas, en z=0 tenes un punto de ramificacion, por lo que no tenes un polo. Esa integral ("5") debe valer 0, proba mayorando o con el teorema que mencionás.
Por el tema de "cerrar" la integral podes probar por ese camino (z = x*e^i*pi) o hacer el packman (en cuyo caso z = x*e^i*2pi). Para distinguir que camino usar reemplaza en la funcion y fijate que te quede un multiplo por la integral que te piden. En el caso de que tengas una funcion par, implicitamente se hace z = x*e^i*pi = x*(-1) = -x, aprovechando de que f(x) = f(-x) para dichas funciones y ese múltiplo es 1 (es decir, vale lo mismo por los negativos que los positivos la integral planteada)
Saludos
Buen día, gracias por la respuesta. Lo de la ramificación y el camino a elegir me quedó claro, de hecho haciendo el reemplazo que proponés llego a una expresión que es efectivamente un múltiplo de la función original.
Lo que no termino de entender es cómo hacer que me queden los límites de integración de 0 a +∞ (no se ve en la imagen pero es lo que se pide originalmente). Según mi desarrollo, al hacer tender R a ∞ y r a 0 la integral que nombro "6" termina siendo múltiplo de la función original, con los mismos límites de integración pero tendría dando vueltas "2" + "4" que va de -∞ a 0 y tendría que calcular eso también. Entiendo el criterio que mencionás cuando la función es par, donde al pasar de -∞ +∞ a, digamos 0 +∞ sale un 1/2 afuera de la integral, no? El tema es cuando no puedo afirmar que la función sea par o análogamente impar, tengo forma de cambiar los límites para que coincida con lo pedido?
Si no me explico lo consulto hoy a la tarde, saludos.
Buenas, ahí mas claro. La que tiene que ser un múltiplo es la que NO es la que te piden. En tu caso, la "6" tiene que ser la que te piden.
Saludos