Buenas tardes! Estoy teniendo algunas dificultades en plantear este ejercicio de series (adjunto el enunciado).
Aunque no estoy muy segura de que sea correcto, llegue a plantear a la función como la suma de dos series de potencias de (z-2) y luego intente de escribirlas a ambas como un desarrollo en Serie de Laurent. En el caso de que fuese correcto, la suma de esas dos series son una serie de Laurent, es decir, eso sería lo que pide el enunciado?
Por el otro lado, en cuanto a la convergencia, creería que converge para todo z menos z=2, pero también, sin muchas certezas.
Muchísimas gracias!
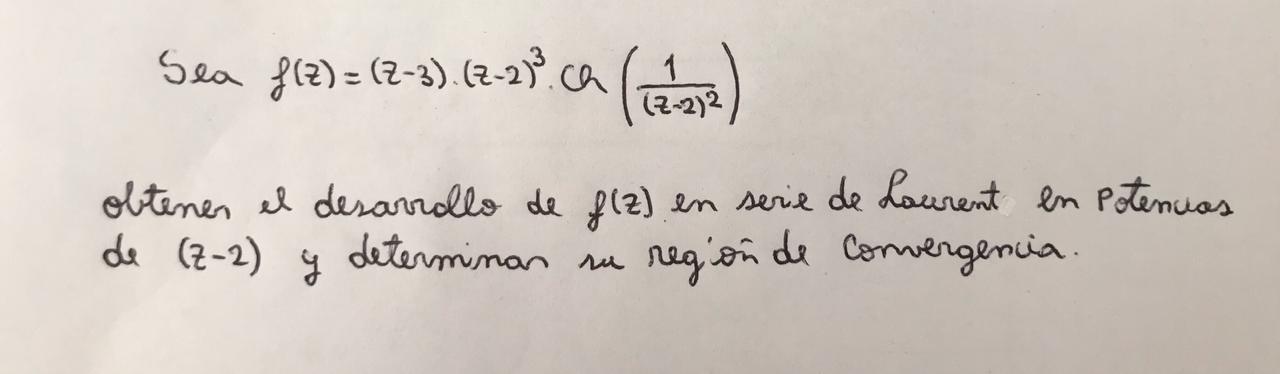

Ahí me doy cuenta que me falto restarle el 2 en las expresiones finales, sería
(z-2)^k y (z-2)^m
Hola. El procedimiento en términos generales está bien. Te hago unas correcciones y comentarios:
Con respecto a la convergencia, hay 3 funciones que se multiplican, la validez de la expresión total es cuando son válidas todas las expresiones simultáneamente (la intersección de las regiones de CV). En este caso los polinomios CV en todo C y el DSL de cosh(1/(z-2)) también es CV en todo el dominio (que excluye a z=2). Eso porque la función no tiene puntos singulares fuera de 2 e infinito.
Donde haces el cambio de variables, como las potencias de z van de 4 en 4, no son solo los pares o los impares los que tenés que anular...podrías poner debajo de cada símbolo de suma, debajo de k=-inf, la aclaración k=-4n+4, n pertenece a los enteros, para dejar expresado que va de 4 en 4. Algo similar en la otra serie.
Y por último te falta poner que f es una serie de laurent de coeficientes c_n dónde c_n=a_n+b_n.
Decime si se entendió es un poco largo.
Hola Julián, se entendió!
Una ultima duda que me queda es, me di cuenta que luego del cambio de variables deje de escribir a f(z) como una resta de series y comencé a escribirla como un suma. Eso es incorrecto no? Al final del desarrollo debería ser f(z) serie de Laurent con c_n=a_n - b_n.
Muchas gracias!
Claro si es una resta de series, te queda que cada coeficiente es la resta de los coeficientes correspondientes
Hola que tal yo tambien me propuse hacer este ejercicio y llegue a algo similar lo que no entiendo es el ultimo paso por que no puedo dejarlo como la sumatoria desde n=0 a infinito y tengo que expresarlo como desde menos infinito a 4 y 3 respectivamente?
Hola, la suma va desde 4 o 3 porque cuando lo multilica por el polinomio, sube el exponente de (z-z_0) a todos los terminos del DSL. Es como si estuvieras haciendo una "distributiba infinita", que es válida donde la serie de potencias CV absolutamente.
Hola, una consulta. Si piden el desarrollo en serie de Laurent, se considera bien dejarlo expresado como suma de series u otra variante?
Depende del ejercicio. Si el enunciado dice "Hallar el DSL" y tu respuesta es una suma o producto de desarrollos, no estarías cumpliendo el objetivo. Si bien a veces es un poco engorroso, si se pide es parte del ejercicio.
Entonces te consulto el siguiente ejercicio. En principio quiero saber si lo que planteo esta bien. Pero final no estoy pudiendo encontrar una expresión que unifique las dos series ya que el patrón para z^-1 no se cumple para todas las potencias.
Y en el caso del residuo que me da "infinito" que puedo concluir? porque no puedo llevarla a una función. Pensé en relacionar con la función Gamma que se puede entender como la función factorial pero no creo que tenga sentido.
El ultimo ítem me pide calcular la integral cerrada sobre |z|=2, es decir, que encierra a z = 0. Que debería hacer con el residuo en z=0?

Buenas, fíjate que hay otra consulta de series en el foro donde pregunte lo mismo y Julián mando foto de como hacer el cambio de variables y unificar las dos series!
Con respecto al punto b) llegue a lo mismo y tampoco supe bien que concluir.
Graciass! No lo había visto. Bueno queda pendiente el b)
Hola. Para el punto b) es eso lo que se pide. Es correcto para el residuo en cero. Para el residuo en infinito, podes usar que Res(0)+Res(inf)=0 y lo sacás por diferencia.
A veces dar una expresión cerrada del coeficiente del DSL para cada valor de n se puede complicar. Se trata de elegir funciones donde eso no pasa, pero no siempre es el caso.
Este es uno de esos casos en los que la expresión es complicada. Como recomendación, si en el examen ven que no pueden llegar a una expresión cerrada, les sugiero dejarlo expresado y retomarlo luego de hacer los demás ejercicios.
