Buenas, como estan?
Quisiera saber si me podrian ayudar con esto. En el punto 4 del TP se pide:
4. Encuentre el punto perteneciente al eje horizontal que corta la recta de acción de la única resultante del sistema.
Yo planteo lo siguiente: Para cada masa encontrar la ubicación del punto que pide de esta forma.
Muchas gracias!
Hola, creo que estas complicando las cosas, es más sencillo el asunto.
Hay que entender que es lo que estas haciendo y luego pasarlo a la planilla.
Nosotros ya reducimos el sistema a distintos puntos, el binomio de R y Mr los tengo para cualquier punto (incluido el origen). Una de las ventajas de utilizar este binomio es que es equivalente a todo el sistema de fuerzas, por lo que es más sencillo trabajar con dos variables que una por cada masa como planteas.
Vamos a tomar la reducción al origen porque es más fácil - podes usar cualquiera - además nos permite ubicar la única resultante respecto al origen. Ahora el problema es buscar puntos en el plano (una recta) donde puedo reducir el sistema y que el momento resultante me de nulo.
Podemos buscar analíticamente la ecuación de la recta pero la idea es tener al menos un punto (el que la recta corta al eje x). Entonces puede tener el siguiente esquema de análisis, xr es mi incognita, estoy en un problema de equivalencia, planteo momento desde el origen y solo me realiza momento la componente vertical de la resultante.
La resultante azul (única) en el punto xr ES EQUIVALENTE al MR0 y R0 ES EQUIVALENTE a todo el sistema de fuerzas.
Cualquier duda volve a preguntar.
Saludos.
Fernando.
Gracias Fernando!
Ahí lo corregí basándome en lo que me dijiste, no había interpretado gráficamente lo que pedía el problema, ahora obtuve resultados que me parecen estan correctos. Me sirvió el grafico que adjuntaste. Ahora me pregunto si hay que realizarlo para cada par de reducción que da el problema.
Adjunto tabla corregida,
Muchas gracias!
Rodrigo, hay algo que estas entendiendo mal.
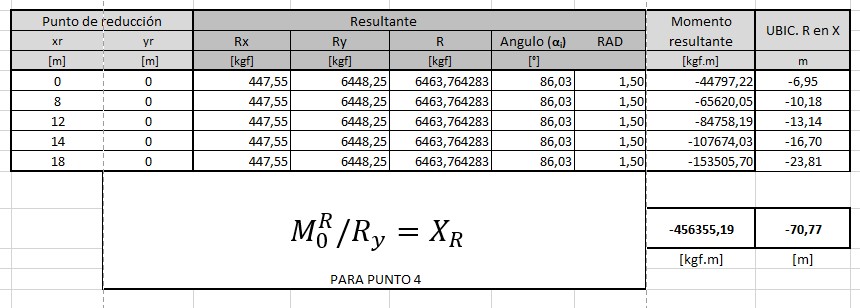
El sistema de fuerzas se puede reducir al punto que vos quieras, en el problema del TP se dan 5 puntos distintos de los infinitos. Cada punto tiene asociado una Resultante y el momento. El sistema y cada una de las reducciones son equivalentes, eso significa que el efecto estático global es el mismo.
EFECTO ESTÁTICO (SISTEMA DE FUERZAS = BINOMIO DE REDUCCION (R Y MR) PARA PUNTO 0 = BINOMIO DE REDUCCION (R Y MR) PARA PUNTO (Xi,Yi)) No conviven, es uno o el otro, por eso es equivalencia.
Ahora de los infinitos lugares donde a uno se le puede ocurrir reducir el sistema hay una recta (cuya dirección coincide con la R) en particular donde el momento resultante es nulo. Es un caso particular. Ese lugar especial es por donde pasa la "única resultante" que quiere decir que la reducción ahí es solo resultante y el momento nulo. No existen varios lugares donde ocurre esto como vos planteas que "depende del punto de reducción", es que siempre te va dar diferente si cambias el punto de reducción con el cual calculas este xr por donde pasa la única resultante. Por eso yo elegí la reducción al ORIGEN para que el valor de Xr que encontras te respecto al cero del problema. Si usas otro punto cambia la relación, el lugar es el mismo. Por ejemplo si para el origen te da xr=10m, tomando la reducción en el punto x=8m el xr=2m.
Lejos de esto, tenes mal los momentos de reducción en los distintos puntos. Por favor chequea tus formulas.
Saludos.
Fernando.
