Hola, quería hacer una consulta respecto a la resolución del ejercicio 3.3.7 de la guía 5 que está publicada en el canal de Youtube del curso.
En el minuto 8, se está mayorando la integral a partir del Teorema de mayoración, concluyendo que para R→∞ la cota es igual a 0:
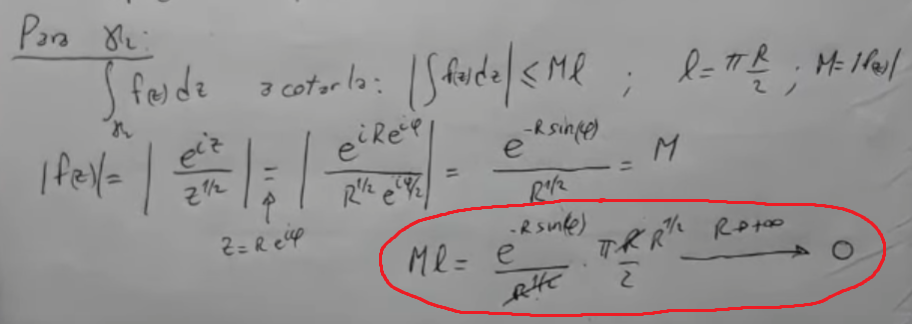
Pero cuando yo lo estaba resolviendo, tuve en cuenta el hecho de que el sen(φ) varía entre 0 y 1 sobre ese camino de integración. De este modo, cuando sen(φ) ≠ 0 mi resultado coincide con lo que se plantea en el video, pero cuando sen(φ) = 0 me queda esto:
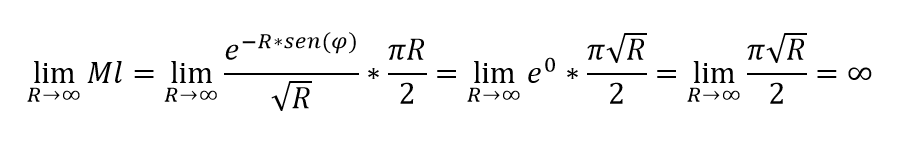
Entonces no es válido acotar la integral con este método, porque resulta menor o igual a algo que tiende a infinito.
¿Me estoy equivocando en alguna parte del razonamiento?
Gracias, saludos.
Hola,
Sí, efectivamente cuando uno mayora la integral, tiene que tomar el máximo valor que el módulo de f(z) toma sobre la curva. En este caso el máximo valor es cuando fi =0, con lo cual si bien es solo un punto, no permite obtener el resultado deseado.
Es decir, no te estás equivocando, está bien tu razonamiento.
En este caso hay que aplicar la siguiente solución:

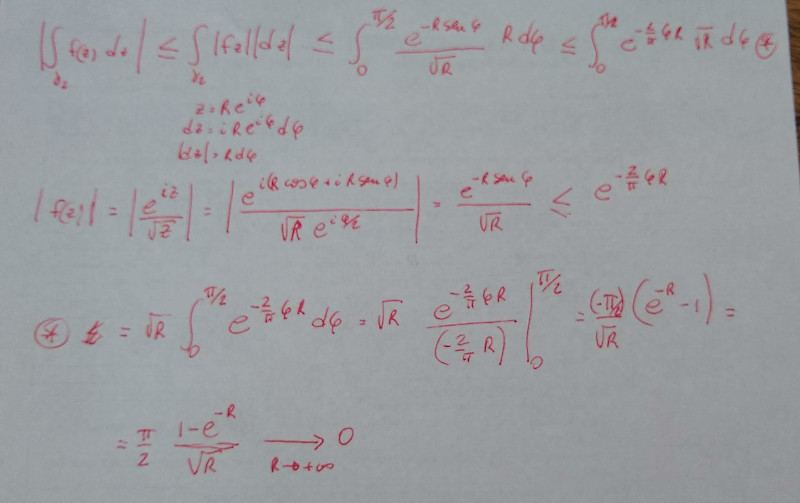
Es decir, no mayoramos con M * L, sino que buscamos mayorar el integrando y luego calcular la integral de lo que queda, pero es conveniente hacer el cambio entre sen(fi) y la recta 2/pi * fi, ya que hace más sencilla la integral.
Avisame si se entiende la idea, y sino trato de explicarlo con más detalle.
Saludos
