Buenos dias, una consulta en relacion al TP1, puede ser que por el mal condicionamiento de la matriz de Hilbert, halla que hacer 72 iteraciones para tener un error menor a 0.1? No se si es un problema del algoritmo que mede tantas iteraciones. Desde ya mucahs gracias.
Saludos.
Raul Chaparro
No te preocupes, debe ser por eso.. A nosotros nos quedó que en el w óptimo necesitaba algo así como 11 mil iteraciones para tener un error menor al 0,001 para una matriz de 5x5; y después quisimos probarlo con 10x10 y llegó a más o menos 43 millones de iteraciones para ese mismo error, así que tranquilo supongo!
Alejandro,
Los números que planteas me parece demasiado grandes. No digo que no puedan ser, pero me parecen muy grandes. Otro grupo me comentó que con una matriz de 5x5 y una tolerancia de 0.01, usando el w optimo, tuvo que iterar entre 600 y 700 veces.
Por favor revisen la implementación para ver que estan haciendo bien las iteraciones.
Sino empiecen probando con una matriz de 3x3.
Saludos,
En realidad nos pasó algo bastante extraño y es que cuando comparamos con el x^k-1 para estimar el error nos da que necesitamos alrededor de 600 iteraciones, pero cuando comparamos con la solución verdadera nos pasa esto de necesitar tantas. Igual usamos el error del pdf que era 0,0001 y no 0,01. También calculamos unas iteraciones a mano y otras en excel y nos dieron lo mismo que con el programa... ¿Puede ser que afecte el hecho de la precisión de las variables (como, por ejemplo, que un resultado dé una cosa pero no se guarde exactamente eso) o será alguna otra cosa?
Hola, si pueden lleven algo para ver hoy después de la clase y lo revisamos.
No entendí tu pregunta final.La máquina va a calcular con el doble de la precisión que hayan declarado en la variable. Esto es así siempre y luego va a guardar con la precisión correspondiente.
Si la precisión de almacenamiento no es suficiente para alcanzar la precisión del resultado exacto, lo que puede llegar a ocurrir es que tal vez la tolerancia es muy exigente y este muy cercana al error de redondeo. En ese caso nunca se llega a una precisión mayor y los resultados pueden comenzar a oscilar alrededor del valor exacto, en este caso.
Lo que se puede hacer es establecer una TOL de corte, pero también una cantidad de iteraciones máxima. Si con un w optimo llegan en 600 iteraciones, podrían establecer una cant. de iteraciones máxima en 6000, por ejemplo.
Saludos,
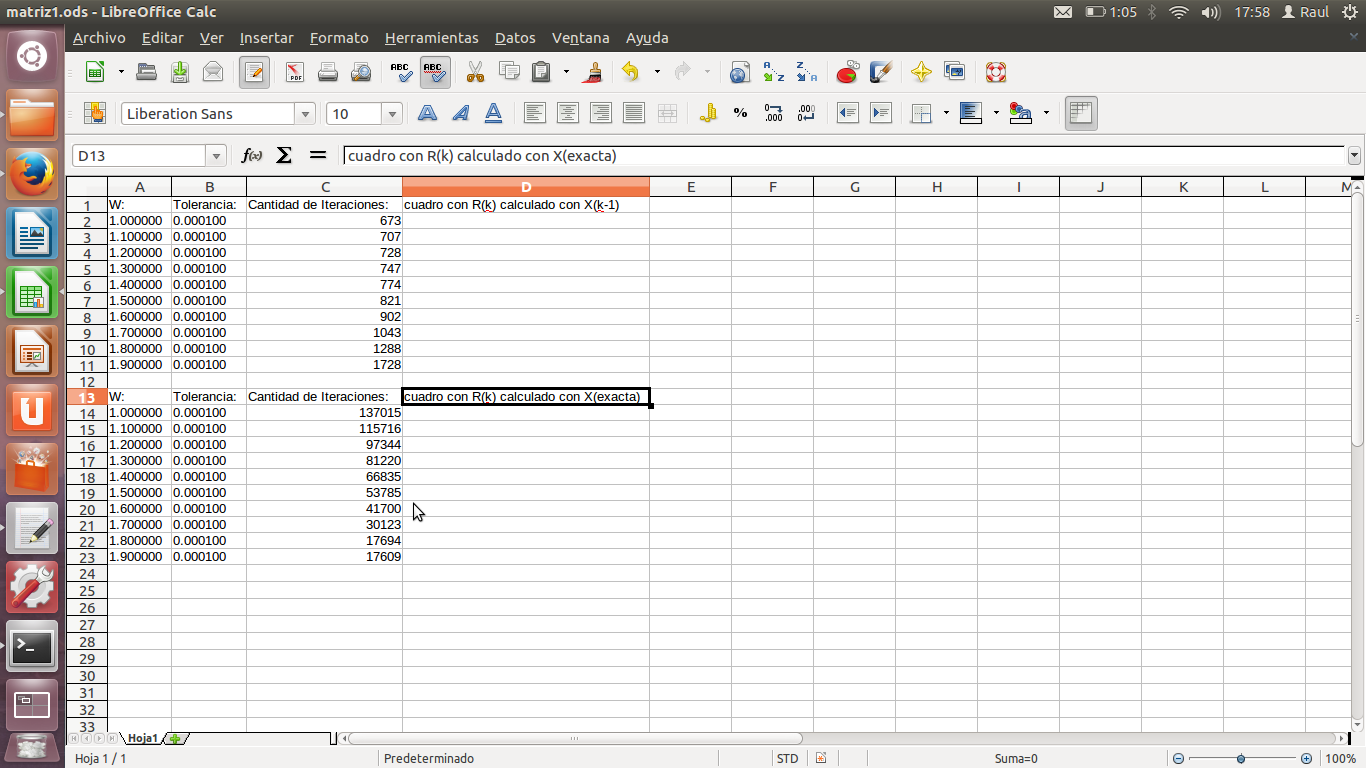
Me sumo a esta consulta tambien, usando una matriz de n=5 y RTOL=0,0001 al usar X(k-1) para el calculo de R(k) me da entre 600 y 700 iteraciones , pero al usar la solucion exacta me da aproximadamente menos de 17000 iteraciones. Adjunto imagen del cuadro en excel.
Hola Raúl,
72 iteraciones no es nada y la tolerancia de 0.1 es bastante baja. ¿Que tamaño de matriz estan utilizando?
Hola buenas tardes, la matriz era de 3x3, y agrego una consulta, puede ser que a medida que vallan trascurriendo las iteraciones el valor de x1 (por ejemplo) valla decreciendo y vuelva a crecer? es decir en la iteracion 1 x1=1,83333, en la iteracion 10 x1=0,6... y en la iteracion 25 x1=0,87.....
Desde ya muchas gracias. Saludos.
