Lamentablemente me fue mal, muy mal... Pero bueno, habrá que ir en otra fecha.
El ejercicio 1 planteaba lo siguiente:

Al transformar por tabla, me quedó
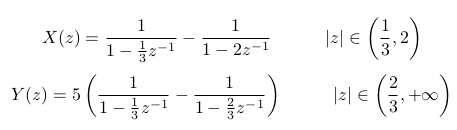
Acá ya encontré el primer problema: yo tenía entendido que en un sistema LTI siempre se cumplía que
![]()
pero en este caso es imposible. Entonces seguí con buscar h[n] para obtener más información y ver de determinar la
ROC. Lo que hice fue simplificar las expresiones y llegué a que
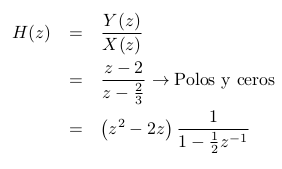
entonces, antitransformando:
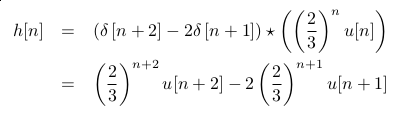
Acá empecé a encontrar más contradicciones:
-- El sistema es no causal debido a que la respuesta al impulso posee valores no nulos para n < 0, por lo
tanto su ROC no es la región exterior a un círculo más el punto en el infinito.
-- La señal es derecha, por lo tanto su ROC es la región exterior a un círculo.
Si su ROC es la región exterior a un círculo (ya que la señal es derecha), se observa que el punto en el infinito está incluido (H(z=infinito) = 1) por lo tanto es una contradicción, ya que sería causal, pero no es causal...
¿En qué me equivoqué?
El golpe anímico con este examen fue mortal, en el momento casi dejo ingeniería jaja
Según lo que entendí yo, la ROC de Y(z) tiene que contener a la intersección de las ROC de H(z) y X(z). La igualdad se dá cuando no hay cancelación de polos, pero en este ejercicio había uno que se si se cancelaba.
Entonces, como la ROC de X(z) era (1/3) < |z| < 2, la ROC de Y(z) era |z| > (2/3), y había dos posibilidades para la de H(z): |z| < (2/3) o |z| > (2/3).
Si |z| < (2/3), la intersección de las ROC de H(z) y X(z) está afuera de la ROC de Y(z).
Por ende, la ROC de H(z) es |z| > (2/3).
Esto fue lo que razoné yo, estaría bueno que alguien me alegre la tarde confirmándomelo.
Hola. Respondiendo a ambos, la única forma de que la ROC de Y no sea contradictoria es que la transformada de H anule el polo que tiene X en z=2 con un cero, el cual termina siendo el caso.
Entonces al hacer la cuenta que hizo Matias, se ve que la ROC de H queda |z|>2/3 y que tiene el cero en z=2 como dice Juan.
Lo que hiciste mal Matías (error de cuentas) fue cuando al polinomio de H(z) lo llevás con el denominador en potencias de z^-1, ya que dividiste por z el denominador (bien) pero MULTIPLICASTE por z el numerador (mal!). Si hacés la cuenta bien termina siendo causal y estable.
Saludos, espero que la tarde de Juan se alegre y que Matias no deje ingeniería por un error de cuentas!
No te la puedo creer!!!En el momento me agarró la calentura mal porque el 2 ya lo había intentado en un parcial y no me salió, el 3 lo sabía hacer (de hecho lo tenía resuelto en un parcial viejo) pero al ver que el 1 no me estaba dando me calenté y me rajé... Es uno de los efectos secundarios de un bajón extra facultad que estoy padeciendo estos días. Simplemente me calenté y me fui...
Gracias por responder Mario, cuando apruebe (la próxima, lo prometo jaja) voy a recomendar tu curso en los foros!!!! Un lujo!
Bueno, éxitos en la próxima que sale y a no chivarse!
