En el siguiente ejercicio:

hay algún truco que no esté viendo? A mi lo único que se me ocurre es plantear que
DFT{x[n]w[n]}[k] = X[k] «convolución circular con» W[k]
La DFT de w[n], W[k], no tengo idea cómo encontrarla por empezar. En el libro no hay tablas de DFT y no creo que haya que hacerlo por definición, no?
Estaba viendo este ejercicio justo. A mi se me ocurrió hacer la multiplicación y después descomponer el coseno en exponenciales complejas.
Llegué a algo así:
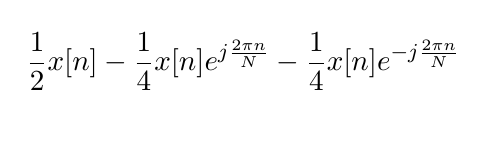
Lo que se me ocurrió después es que la x[n] por las exponenciales parecerían ser DFT corridas circularmentes. ¿Pero la DFT de qué? Asumo que habría que usar dualidad, pero no me queda muy claro cual debería ser el resultado.
Hola. Lo que planteás es correcto. La DFT de qué hay que correr circularmente preguntás, es la DFT de x(n) de N puntos.
Para la pregunta anterior, que no sabía cómo encontrar la DFT de w(n), la podés plantear por definición que sale fácil o sino como las muestras del espectro de w(n) cada 2pi/N puntos. El espectro de w(n) es fácil de encontrar, son 3 sincs de centradas en las frecuencias Omega=0, Omega=2*pi/N y Omega=-2*pi/N.
Saludos
Listo, hicimos esto. A partir de acá se puede seguir usando la propiedad 6 de la tabla que está en el Schaffer, la de W_N^{-ln} y queda hermoso. Nos quedó
DFT_Npuntos{x[n]w[n]} = X[k]/2 -1/4*(X[((k+1))_N] + X[((k-1))_N])
Sabiendo qué hacer era muy fácil el ejercicio jaja
