Publicar en este hilo cualquier consulta relacionada con la Unidad 2

Hola, estaba repasando y me encontré con una duda que me quedo sin consultar. Como se haría en este caso para representar el error producido por sacar el coseno, o cualquier valor en general, por tabla con cierta precisión; es decir, cual seria mi factor de amplificación, error de maquina, etc.
Tomás,
Normalmente en cada operación de la gráfica de proceso hay un factor de amplificación (que se puede sacar de tablas o deducir), y un error de redondeo, que normalmente está siempre acotado por la unidad de máquina.
En este ejercicio tenés la particularidad de que el error de redondeo para la operación del coseno es distinto de todos los otros (5 decimales significativos vs 7 dígitos de precisión). El factor de amplificación del coseno los tenés que sacar de tablas o deducir, como en cualquier otra operación.
Saludos
Hola que tal?
Estaba resolviendo el ej 2.10 y no me queda del todo claro cuando se despeja E1*n1/(n1+a)=2/3 E1... Adjunto imagen de la parte del fragmento de la explicación de youtube donde se realiza este despeje!
Desde ya muchas gracias
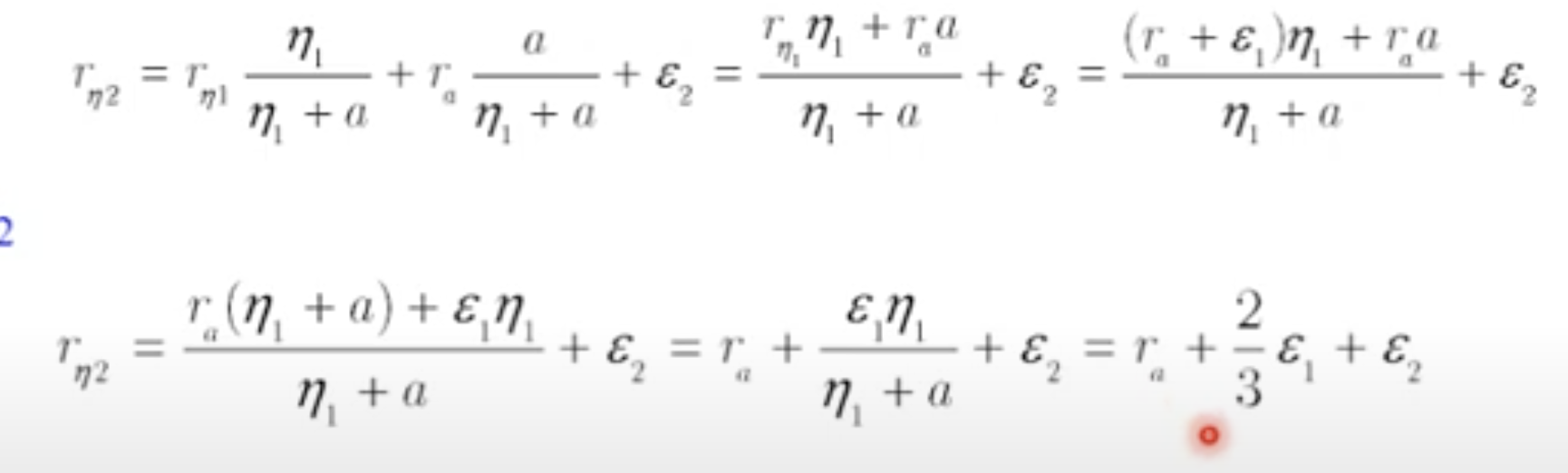
Es muy sencillo: no es otra cosa que
. Por lo tanto tenés
en el numerador y
en el denominador. La
arriba y abajo se cancela, y queda 2/3.
Saludos
Gracias! Es verdad, no lo había visto.
Aprovecho para hacer dos consultas mas.
La primera es del ejercicio 14. En el punto b llegué a y para que el error de redondeo sea despreciable frente a los errores de entrada pensé que el termino que contiene u sea menor al que contiene R, de modo que
se cancela de ambos lados y puedo llegar al mismo resultado que esta en el resuelto del campus. Lo que no me cierra es que en dicho resuelto se plantea que si f1 y f2 son del mismo orden,
. Eso no me parece evidente viendo la ecuación que define f0 y no termino de entender por que se lo puede afirmar.
La ultima duda es del ejercicio 13. Llegue a las expresiones de factor de amplificación de redondeo para el primer algoritmo y
para el segundo. Le pregunte al profesor Menéndez en la teórica si bastaba con reemplazar con algún a cualquiera y comparar los dos factores así, pero el profesor me recomendó que use las series de Taylor y el hecho de que <0a<<1 para simplificar las expresiones y compararlas de forma general. Se me complica ver como proceder de esta forma.
Espero que se entiendan las consultas, desde ya muchas gracias!
Hola Lara
Sobre el ejercicio 14: Acordate que los errores basta con calcularlos de manera muy aproximada (solo necesitamos un dígito de precisión). Por lo tanto, como el enunciado dice que y
son del mismo orden, podemos asumir que son casi iguales (
también, porque es un valor intermedio entre los otros dos).
Sobre el ejercicio 13: Lo que propone Ángel es bastante fino, pero no necesariamente da resultado: pensar que cada factor de amplificación es una función de : por ejemplo
en el primer caso y
en el segundo; luego desarrollar un polinomio de Taylor para cada una:
Obviamente calculando las derivadas correspondientes para cada caso. lo podés tomar como quieras (en principio creo que un valor de 1 sería conveniente). Ambos polinomios pueden luego compararse entre sí, y ver si se nota que uno sea sistemáticamente mayor que el otro. Como dije arriba, esta técnica puede dar o no una conclusión.
En la práctica efectivamente podés hacer como vos propusiste; probar distintos valores de y comparar los valores que resultan.
Saludos
Buenas en el ejercicio 4 y 6 preguntan sobre la incidencia del error de cada una de las variables, es decir, cual es mas relevante al momento de sumar todo. Llegué a varias conclusiones pero estoy seguro de que solo hay una correcta. Por ejemplo, no se si al momento de responder es el factor de amplificación el que importa o todo el error que suma la variable. Espero se entienda, muchas gracias.
Hola Gonzalo. Se entiende la pregunta. En realidad las dos maneras de pensarlo son correctas desde distintos puntos de vista. Si uno NO conoce el error relativo de cada variable, entonces el factor de amplificación sería la medida a adoptar. Si en cambio SI se conoce el error inherente de cada una (creo que en el problema es así), entonces habría que comparar el factor de amplificación una vez multiplicado por ese error.
Saludos
Hola, en el ejercicio 13 pensé resolverlo buscando el número de condición de cada algoritmo para ver cuál es más estable, pero no se que factor de amplificación usar cuando por ej me dan una raíz.
Los factores de amplificación para cualquier función f(x) se pueden deducir fácilmente. Está explicado en una de las clases, pero, brevemente, el procedimiento es así:
Ecuación (1):
Usando la fórmula de propagación de errores inherentes se obtiene (2):
Ahora se divide (2) por (1)
Se multiplica y divide por x el término de la derecha
Finalmente:
Hola, en el ejercicio 6 en el ultimo inciso me pide que el error relativo sea menor al 10 porciento… Po lo que tenia entendido la definición de este era error exacto sobre valor exacto. Mi duda es que si en este caso yo tengo que hacer el cociente de la cota de error (delta x) sobre el valor estimado y esto multiplicarlo por 100, este porcentaje tiene que ser menor al 10 porciento así que ya me quedaría para sacar delta i, correcto?
Hola, en el ejercicio 9 tenia una dudas sobre el planteo. Hice esto pero no se si esta bien… primero hice un diagrama y tuve en cuenta el error de redondeo U de la raíz cuadrada tal que quedé con 6 decimales.
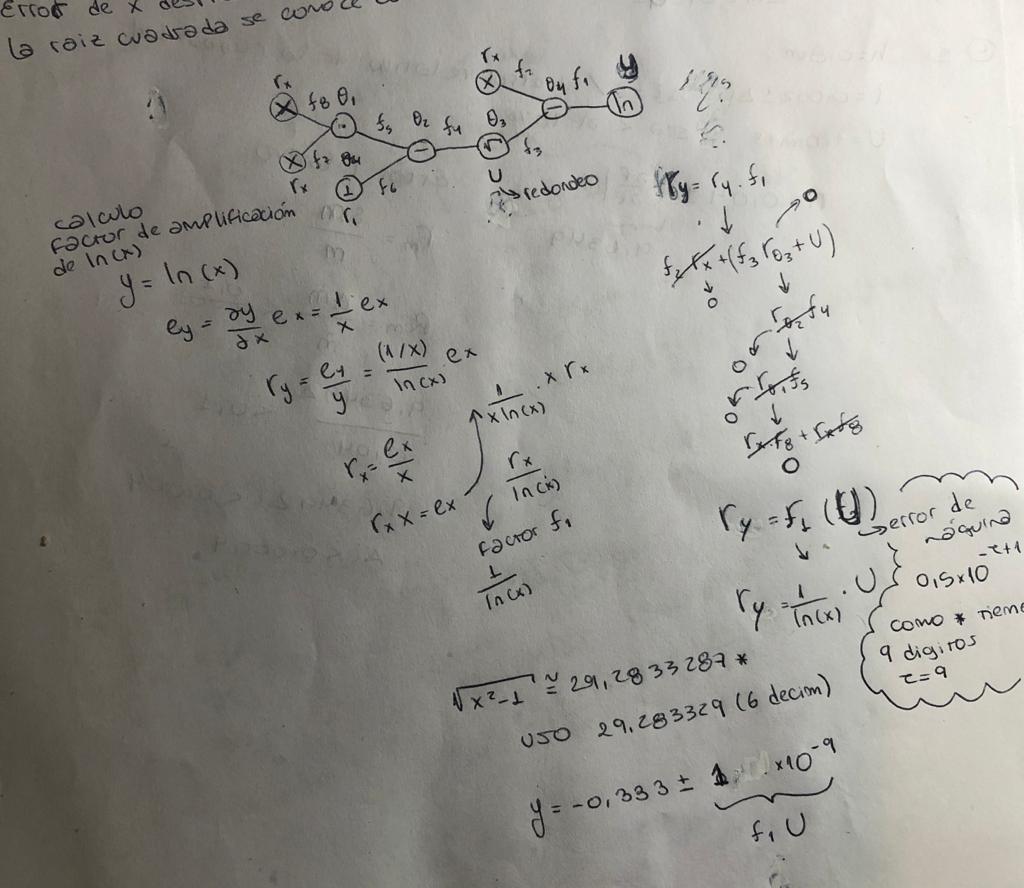
Hola, en el 9 b me piden resolver w=(a/c)-(b/c) con a=0,41 b=0,36 y c=0,70 con redondeo a dos dígitos.
Si yo hago a/c me da 0,59, luego b/c=0,51 y 0,59-0,51 da 0,080 pero en el resuelto dice w=0,071. ¿Qué estoy haciendo mal o está mal el resuelto?
