Buenas tardes,
hice este ejercicio primero en papel y luego quise resolverlo en R con la librería lpSolve, pero me está dando algo que no tiene sentido (el porcentaje de cada metal no me da 100%). ¿Alguno me podría decir si es que está mal planteado el modelo o si le estoy pifiando a algo en el código?
Adjunto fotos del planteo y el archivo de R.
Muchas gracias


Me sumo a la consulta. Yo lo resolví de una forma distinta (sin variables totalizadoras) y tengo el mismo problema, los resultados finales de A-B-C-D no me llegan a sumar el Kg de aleación.
Adjunto la imagen del planteo y el archivo R. (Para las restricciones con desigualdad de <= al escribirlas en R multiplique por -1 para transformar todas en >=)
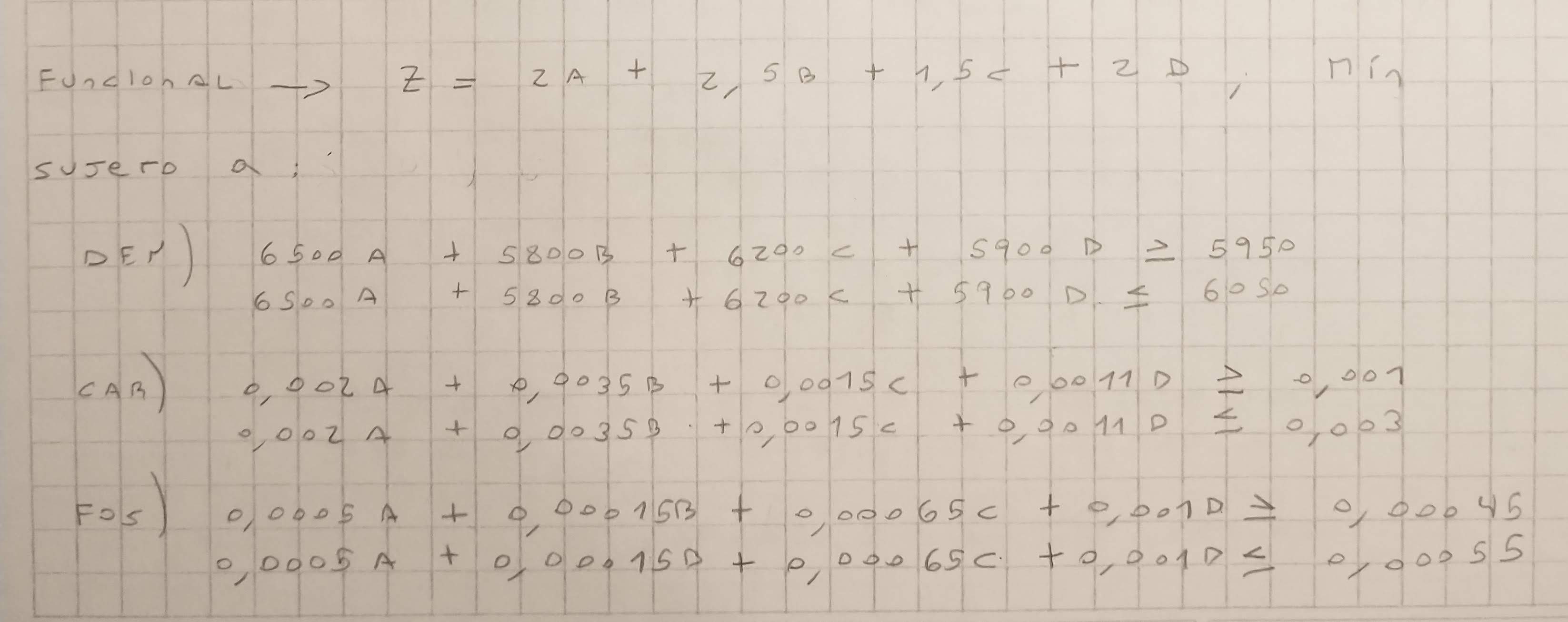
Creo que deberías agregar una restricción más que sea: A+B+C+D=1.
Adjunto lo que me dio en R.
las restricciones son las mismas en todos los casos.
Me dio esto
Utilizar 0.0 A
Utilizar 0.21312376 B
Utilizar 0.79697144 C
Utilizar 0.0 D
Valor Optimo: 1.7282665599999998
CODIGO
Yo no utilice totalizadoras , pero pedí que la sumatoria de metales sea 1 Kg, ya que el costo que me daba era en $/kg.
Además tome los valores del enunciado como si ya fueran dados en porcentaje, no los dividí por 100.
Me dio Z=1.8444828 , XA=0; XB=0.284483, XC=0.594828; XD=0.12690
Dejo mi modelización en Lindo, y adjunto el Script de R.
MIN 2XA+2.5XB+1.5XC+2XD
ST
XA+XB+XC+XD=1
!Restricción de densidad
6500XA+5800XB+6200XC+5900XD<6050
6500XA+5800XB+6200XC+5900XD>5950
!Restricción sobre % carbono
0.2XA+0.35XB+0.15XC+0.11XD>0.1
0.2XA+0.35XB+0.15XC+0.11XD<0.3
!Restricción sobre % FÓSFORO
0.05XA+0.015XB+0.065XC+0.1XD>0.045
0.05XA+0.015XB+0.065XC+0.1XD<0.055
END
Era la restricción de la sumatoria que me faltaba, gracias!
Buenos días,
estaba revisando este ejercicio ayer y leyendo las respuestas acá vi que algunas resoluciones plantean la restricción de la densidad máxima y mínima así:
6500XA+5800XB+6200XC+5900XD<6050
6500XA+5800XB+6200XC+5900XD>5950
y no entiendo bien por qué. El resultado final de las Xi me da muy cercano pero no me termina de quedar claro por qué se multiplican las cantidades Xi, que entiendo están en kg, por la densidad, que tiene unidades de masa/volumen, no me cierran las unidades que quedan.Si alguno de los que lo planteo así me lo puede explicar se lo agradecería.
Yo en realidad no pensé mucho en el tema de la unidad de la densidad, por qué como no te da volumen ni nada de los metal, no veía como relacionarlo. Lo pensé directamente de la forma "6500 DEN/kg". Osea sin darle muchas vueltas a que representaba DEN.
No sé igual si esta bien ese razonamiento
Felicitaciones a todos los que participaron en este intercambio! Agradecemos los comentarios y el material.
El tema de las unidades de X surge porque no se definen bien las variables,
Especificar bien las variables es super importante para verificar la correctitud de los modelos que imaginamos.
En el caso del problema, si recuerdo bien...
X es proporción, es decir que no tiene dimensiones, aunque hay que aclarar que es en volumen. Por ej: X cm^3 de A por cada cm^3 total.
Entonces la densidad de la mezcla sí es la combinación lineal de las densidades, y las unidades (imaginen g/cm^3) cierran, porque agrego X[cm^3/cm^3] de cada componente. Eso suponiendo aditividad de masa y volumen en una aleación metálica.
Me avisan si hay mas dudas.!
Hola!, yo lo hice considerando las unidades, o sea con las restricciones 5950.volumenproducto<=1 y 6050.volumenproducto=>1. considerando el volumen del producto como la suma de los volúmenes de A, B,C y D.
Me da lo siguiente:
OBJECTIVE FUNCTION VALUE
1) 1.823261
A 0.000000
B 0.246887
C 0.600365
D 0.152748
Adjunto código en LINDO:
!Problema 2.1
!variables:
!A: Kg de A
!B: Kg de B
!C: Kg de C
!D: Kg de D
!considero peso del prodcuto 1 KG.
!funcional
min 2A+2.5B+1.5C+2D
Subject to
A+B+C+D=1
0.002A+0.0035B+0.0015C+0.0011D>=0.001
0.002A+0.0035B+0.0015C+0.0011D<=0.003
0.0005A+0.00015B+0.0006C+0.001D>=0.00045
0.0005A+0.00015B+0.0006C+0.001D<=0.00055
!5950*Volumen del producto<=1
0.91538A+1.02586B+0.959677C+1.008474D<=1
!6050*Volumen del producto>=1
0.930769A+1.043103B+0.9758064C+1.0254237D>=1
end
Gracias por Compartir!
También me estaba faltando agregar la condición A + B + C + D = 1
Es esa restricción le que da sentido a la definición que se hace para las variables de decisión, que son fracciones (en volumen) del total de la aleación final.
Dejo los resultados obtenidos en python y el script adjunto.
IO_Ej_Guia_2.1:
MINIMIZE
2*XA + 2.5*XB + 1.5*XC + 2*XD + 0.0
SUBJECT TO
restriccion_Densidad_MAX: 6500 XA + 5800 XB + 6200 XC + 5900 XD <= 6050
restriccion_Densidad_MIN: 6500 XA + 5800 XB + 6200 XC + 5900 XD >= 5950
restriccion_Carbono_MAX: 0.2 XA + 0.35 XB + 0.15 XC + 0.11 XD <= 0.3
restriccion_Carbono_MIN: 0.2 XA + 0.35 XB + 0.15 XC + 0.11 XD >= 0.1
restriccion_Fosforo_MAX: 0.05 XA + 0.015 XB + 0.065 XC + 0.1 XD <= 0.055
restriccion_Fosforo_MIN: 0.05 XA + 0.015 XB + 0.065 XC + 0.1 XD >= 0.045
restriccion_Suma_de_fracciones: XA + XB + XC + XD = 1
----------------------------------------------------------------------
Valor Optimo del Funcional:
objective: 1.8448276049999999
XA: 0.0
XB: 0.28448276
XC: 0.59482759
XD: 0.12068966
restriccion_Densidad_MAX: 5.999999962114089e-05
restriccion_Densidad_MIN: 100.00005999999962
restriccion_Carbono_MAX: -0.09793103290000002
restriccion_Carbono_MIN: 0.10206896709999999
restriccion_Fosforo_MAX: 7.499999996052331e-10
restriccion_Fosforo_MIN: 0.010000000749999995
restriccion_Suma_de_fracciones: 9.999999911469715e-09
